もくじ
ポイント
平行四辺形であると言えるか?→何をすればよい?
平行四辺形になる条件5つを思い出そう。
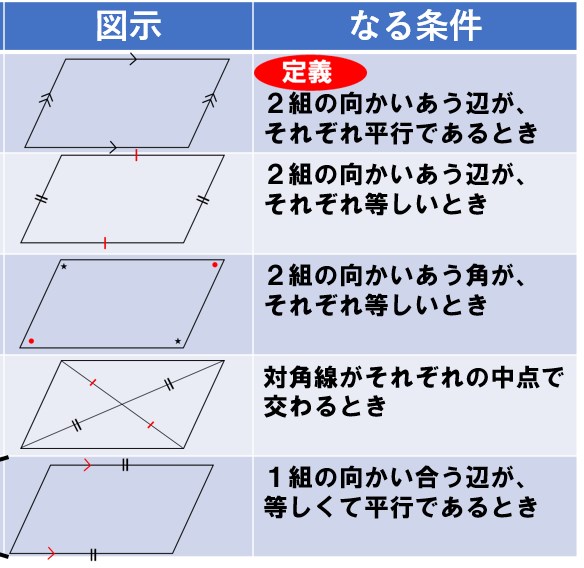
この5つの条件の内、どれか1つでも成立すれば、その四角形は平行四辺形であると言えるよ。
逆に、1つも成立しなければ、平行四辺形ではないよ。
必ず図を書くこと
図を書かないと絶対にわからない!
四角形ABCDのかき方に注意!
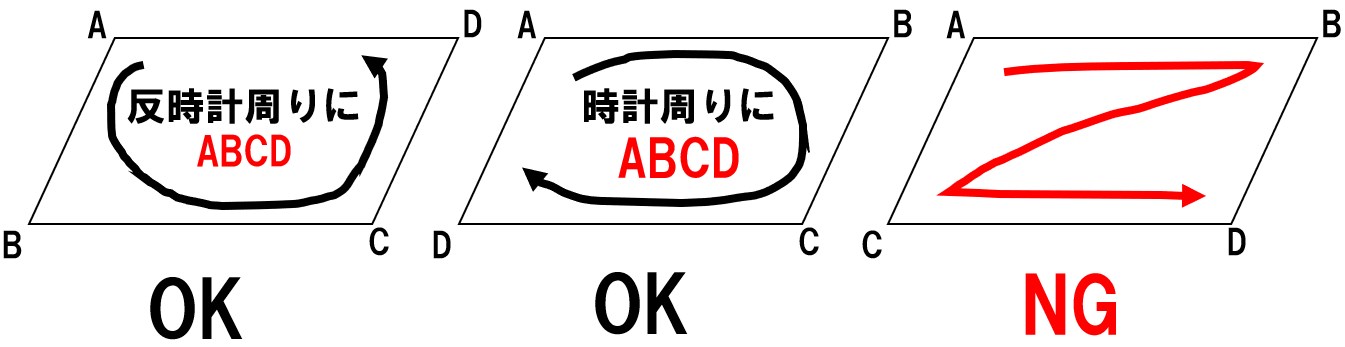
反時計回りにABCDと付けるか、時計回りにABCDと付ける。
これ以外はNGです!
角度や長さは気にしないで図示する
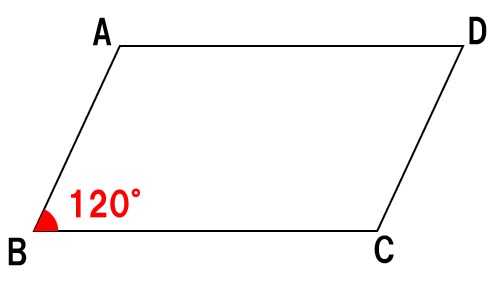
角度や長さを図示していくと、上の図のように、90度より小さいのに120°と書かないといけなかったりするけど、
とりあえず、気にせずに角度や長さを四角形ABCDに書き込んでいこう!!
「平行」と書かれていたら、同位角や錯角がカギとなる
AD∥BCなどと記載があれば、同位角や錯角を利用することが多いよ!
同位角や錯角は、もちろん覚えているよね?
 中2数学:同位角・錯角・平行線のまとめ
中2数学:同位角・錯角・平行線のまとめ
解き方
(1)AB=4, BC=8, CD=8, DA=4
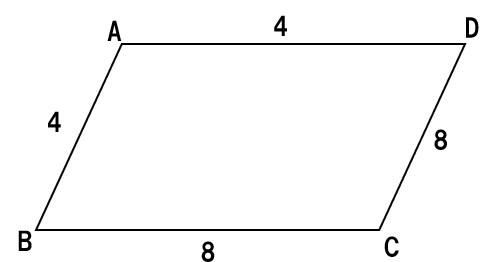
向かい合う辺の長さが等しくないので、平行四辺形ではない。
(2)∠A=∠D, ∠B=∠C
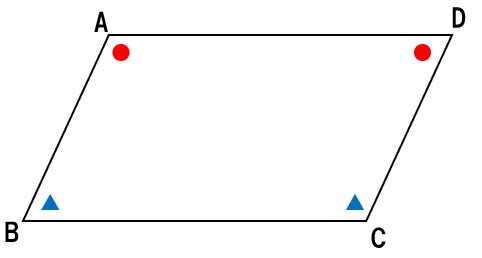
向かい合う角が等しくないので、平行四辺形ではない。
(3)AD∥BC, ∠B=∠D
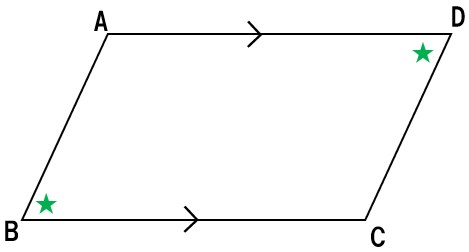
この問題は少し難しいよ。先に解き方を説明します。
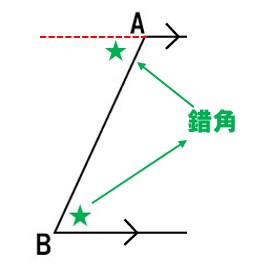
AD∥BCなので、ADを延長すると、上の図のように等しい錯角が表れる。
この錯角は、∠Dと等しい。
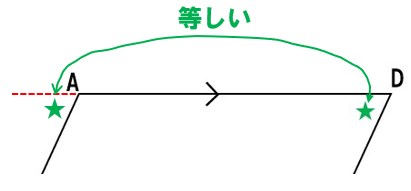
★の同位角が等しいので、AB∥CDである。
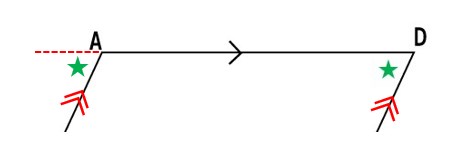
よってAD∥BC、AB∥CDなので、
2組の向かい合う辺が、それぞれ平行であるので四角形ABCDは平行四辺形である。
<補足:考え方>

感覚的に、ABCDは平行四辺形になりそうだとわかるかな?
向かいあう角(★)が等しくて、ADとBCは平行だからね。
じゃあ、5つの条件の内、どれを示そうか・・・・?
ポイントは「平行」という仮定があること
→きっと、平行の条件を使うだろう。
→5つの条件の内、平行の条件が入っているのは以下の2つだけ。
- 2組の向かいあう辺が、それぞれ平行であるとき
- 1組の向かい合う辺が、等しくて平行であるとき
だから、どちらかを示せればよいと考える。

だから、「2組の向かいあう辺が、それぞれ平行である」←こっちを示せばよいと考えるんです!!
(4)∠A=115°∠B=65°AD=4, BC=4
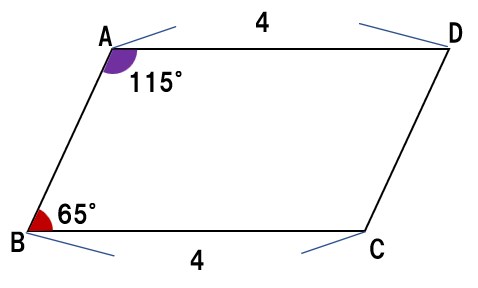
この問題も少し難しいかも。先に解き方を説明します。
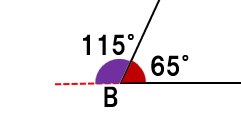
BCを延長すると、∠Bの外角は115°
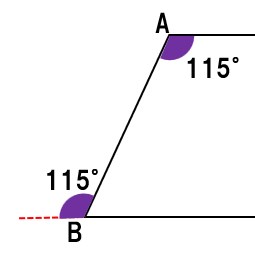
上の図のように、錯角が等しい。
よって、AD∥BC
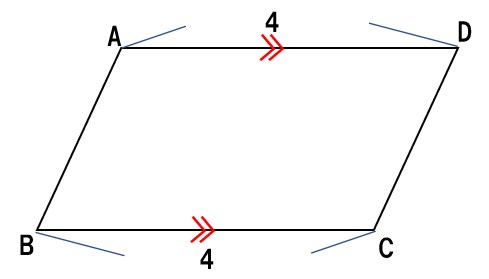
よって、1組の向かい合う辺が、等しくて平行であるので、四角形ABCDは平行四辺形である。