「授業わかるーの」運営者のナオドット先生です。
MEMO
この記事は、とーっても評判が悪かったので(わからないという感想が多い)内容を大きく変えてみたよ!2022/11/2変更済み
逆ってなんだ??理解すれば単純なので安心して!!
もくじ
逆とは?
逆の定義は、
- 「仮定」と「結論」を入れ替えたもの
「●●ならば★★である」
これの逆は
「★★ならば●●である」
逆をいいなさい。という問題がきたら
逆を言え。という問題が来たら、こうやるんだ!丸暗記すること!
↓↓
「逆を言いなさい」問題は
●● と ★★を入れ替える
逆が成り立つか?
逆は、文章を逆にしちゃうよね?
だから、逆にした文章が成り立つときと成り立たないときの両方があるんだ。
①逆が成り立つとき
「三角形の3辺の長さが全て等しいならば、正三角形である。」
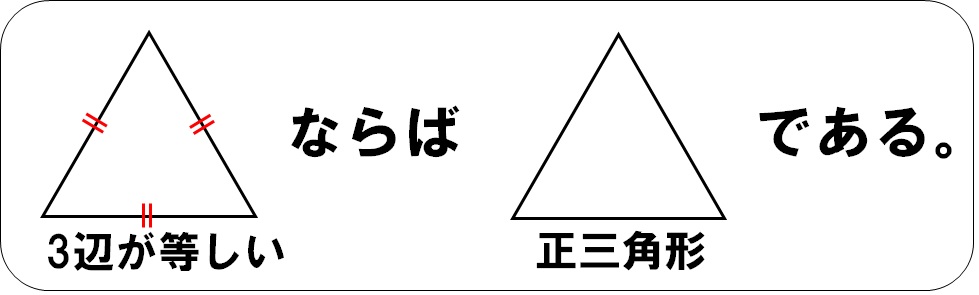
これの逆は
「正三角形ならば、三角形の3辺の長さが全て等しい。」
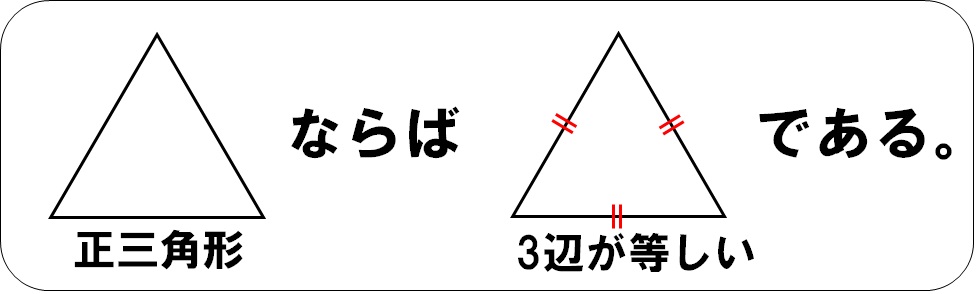
「逆」は、成立する。
正三角形は、必ず3辺の長さが等しいので!
②逆が成り立たないとき
「ハトならば、鳥である。」

これの逆は
「鳥ならば、ハトである。」

「逆」は、成り立たないんだ。
だって、鳥には、「ツバメ、すずめ、かもめ」いっぱいいるからね。
反例とは?
逆が成り立たないとき、当てはまらない「例」のこと。
例えば、
- ハトならば、鳥である。
- 逆:鳥ならば、ハトである。
- 反例:ツバメ
逆の練習問題
次のことがらの逆をいいなさい。また、逆が正しいか調べなさい。

(1)△ABC≡△DEFならば、∠A=∠Dである
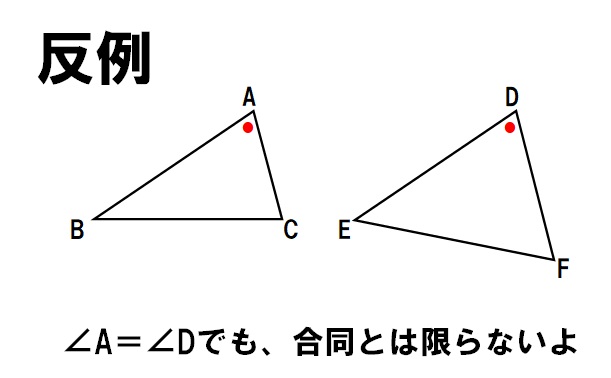
- 逆:∠A=∠Dならば、△ABC≡△DEFである。
- 逆が正しいか判断:正しくない
(2)△ABC≡△DEFならば、AC=DFである
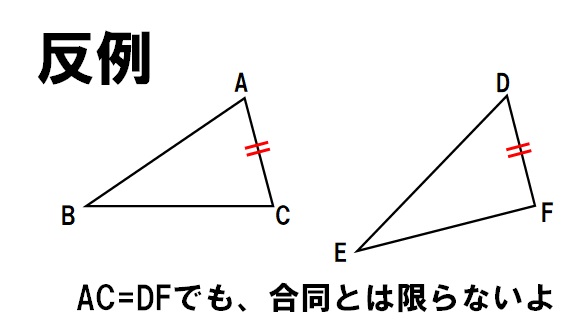
- 逆:AC=DFならば、△ABC≡△DEFである。
- 逆が正しいか判断:正しくない
(3)2つの角が等しい三角形は、二等辺三角形である
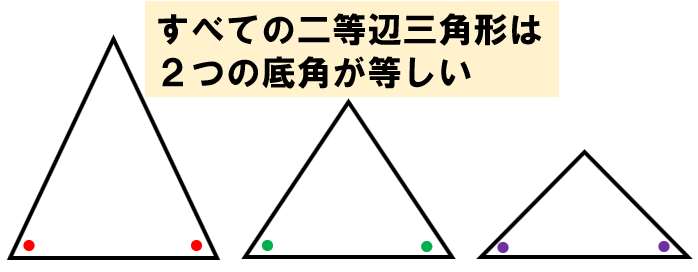
- 逆:二等辺三角形ならば、2つの角が等しい三角形である。
- 逆が正しいか判断:正しい
(4)𝒂>0, 𝒃>0ならば、𝒂+𝒃>0である
- 逆:𝒂+𝒃>0ならば、𝒂>0, 𝒃>0である。
- 逆が正しいか判断:正しくない

次の学習は直角三角形の合同、証明だ!難易度は「中」くらいだね
理解できた?

質問があればお気軽にどうぞ。100%返答します。
x+1=3ならばx=2であるの逆は成り立ちますか?
はい。逆は成り立ちます。
逆:x=2ならばx+1=3である。
x=2のとき、x+1=2+1=3 となり、疑いなく成り立ちます。
いろいろと事情がありまして、現在定期テストのみ登校し、家庭にて一人で全ての勉強を行なっている者です。
たとえば、
aの2乗=bの2乗である。の逆、また、正しければ○を、正しくなければ反例を示しなさい。 という問題などで、逆は間違いなく書けるのですが、反例などが思いつかなかったり、正しいかすぐにわからなかったりします。他のこの形式の問題も同様です。
すぐに正誤がわかるような考え方のコツはありますでしょうか?
一人で学習するのは大変ですよね!
「逆」が正しいかどうか?すぐに正誤を判断する裏技はありません。
問題を複数解いて、慣れる必要があります。
頭だけで考えて正誤判断をしないことです。紙に書いてみましょう。
例えば、
・図形問題なら実際に図を描いてみる
・数式なら具体的な数字を当てはめて考えてみる
・数値問題なら+-に落とし穴がないか、あてはめてみる
基本的なことですが、確実にやる。さらに問題を複数解いていく。
地道な努力が必要です。
頑張ってください!
授業で先生に、サルなら動物である→動物ならサルである×
「サルの惑星になってしまう」という例えで教えてもらいましたが、動物なら猫も犬もいるよね、、、ここまでは分かったのですが、ほかの問いになると反例を見つけられません!書き方がわかりません!どうしたらいいですか?
テスト前なのにピンチです(;´Д`A “`
コツというコツは無いのですが、やはり慣れしかないです。
整数の問題などでは、-(マイナス)のときはどうか?という視点を持つことが大切です。