中２数学：証明問題（平行な２直線→三角形の合同を用いた証明）

証明問題の例題だよ！一歩ずつやれば、必ず解けるから安心して、一緒に解いてみよう！

ポイント

最終的にAE＝CEであることを示したいわけだよね？

でも、AE＝▲▲cm、CE=▲▲cm　→　ほーら、同じ長さだよ！とは証明できないんだよね・・・！

なぜなら、長さ寸法は問題で一切与えられていないから。

だから、別の方法を用いて間接的にAE=CEであることを示す必要があるんだ！！

別の方法って・・・？

三角形が２つあるよね？？しかも、同じような形をしてるよね？？

先に答え（証明の流れ）をいっちゃうと

三角形が合同 → だから辺の長さは等しい

という証明の流れになるんだ！では、具体的に見ていこうね☆

解き方

これまでの３ステップに加えて、ステップ2-2を追加したよ！

解き方の流れはこんな感じだね↓↓

ステップ1：「仮定」と「結論」を整理する
ステップ2-1：「仮定」を図示する
ステップ2-2：「仮定」から新たに分かったことを図示する
ステップ3：何を示せば「結論」にたどりつけるか考える

仮定と結論の整理

ここは大丈夫だよね？

●●ならば、★★だ。というのが「仮定」と「結論」だったね。

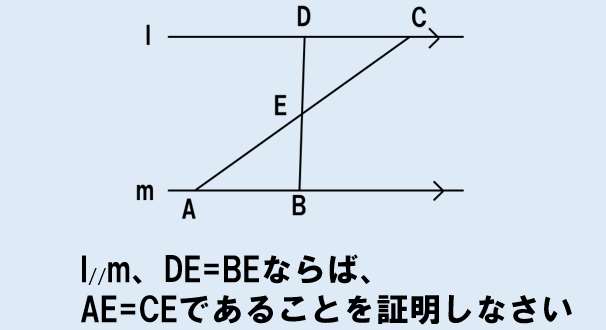
仮定：l //m、DE=BE
結論：AE=CE

仮定を図示

２つの仮定を、図示するよ！
↓↓

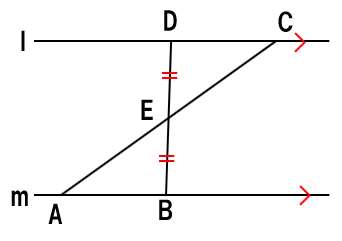
仮定から新たに分かったことを図示

新たに何がわかる？

新たにわかることは２つだ！

２直線は平行 → 錯角と同位角が等しい
辺DBと辺CAは交差 → 向かい合う角（対頂角）が等しい

錯角と同位角が等しい

図を見る限り、同位角は無さそうだね。

錯角は２か所あるよ！図示してみると・・・

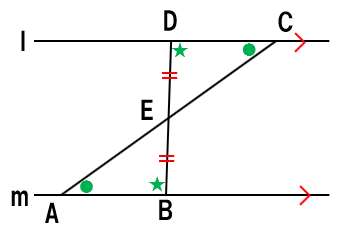
錯角は「Z」と「逆Z」だったよね。

錯角や同位角を忘れちゃったなら、必ずここで復習してね！

参考：同位角・錯角・対頂角・平行線のまとめ

対頂角が等しい

∠AEBと∠CEDは対頂角なので等しい！

図示するよ。

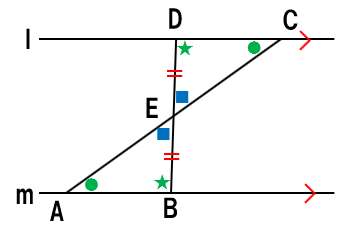
何を示せば「結論」にたどりつけるか

結論にたどりつくには、２つの三角形が合同であることを示せばいいんだよね？

「仮定」の条件をもとに、図示した図をもう一度見てみようね！

三角形の合同条件、何が使えるかな・・・？

「＝」と「■」と「★」　が使える！

（今回「●」の役目は無かったね。こういうこともあるドンマイ！）

BE=DE、∠AEB＝CED、∠ABE=CDEだから、

１組の辺とその両端の角がそれぞれ等しいので、△ABE≡△CDE

合同な図形では対応する辺の長さが等しいので、AE=CE・・・（終わり）

はい次！次は二等辺三角形について学んでいこう！

中２数学：二等辺三角形の基礎（角の大きさ、二等分線、合同を用いた証明）

理解できた？