中２数学：証明の基礎(仮定・結論・三角形の合同を利用)まとめ

苦手な生徒が多い証明問題に入っていくよ！

実はそんなに難しくないんだ。学校の先生から、難しく教えられているだけだよ・・・（汗）

さ、順番に見ていこう！！

証明の基礎

証明ってそもそも何？？？

証明は、「正しい」ってことを示すこと。

仮定と結論

２つの大事な言葉、「仮定」と「結論」

●●ならば、★★だ。　

• 「仮定」：●●　の部分
• 「結論」：★★　の部分

証明の手順

●●ならば★★だ。

三角形の合同条件などを使って、結論の★★が正しいことを示す。

証明のやり方（例題）

実際に問題をやってみた方が、しっくりくると思う。なので、基礎的な問題を一緒に解いてみよう！

ざっくりした手順はこんな感じ↓↓

• ステップ1：「仮定」と「結論」を整理する
• ステップ2：「仮定」を図に書き込もう
• ステップ3：三角形の合同条件などを使って「結論」が正しいことを示す

ステップ1：「仮定」と「結論」を整理する

●●ならば★★だ。なので、仮定と結論は次の通り。

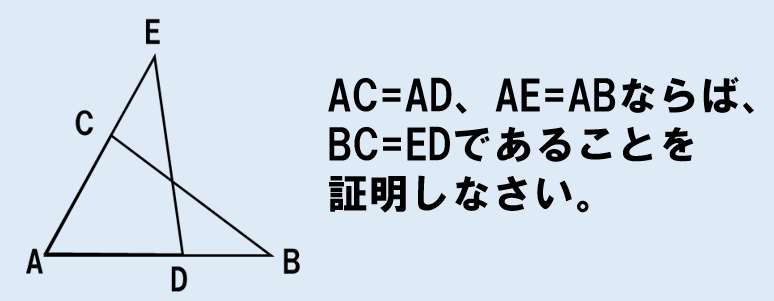
• 仮定：AC=AD、AE=AB
• 結論：BC=ED

ステップ2：「仮定」を図に書き込もう

次は、仮定の内容を、図に書き込んでみよう。

仮定は２つで、AC=AD　と　AE=AB　なので図示すると

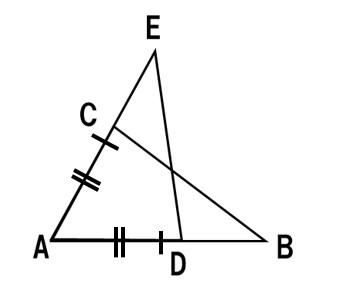
とてもわかりづらいので、説明のために分けて色をつけて書いてみるよ！

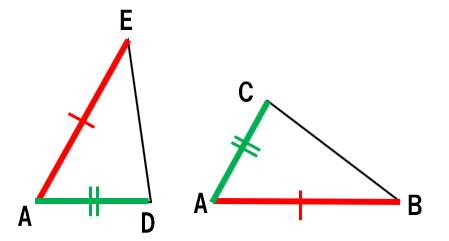
ステップ3：三角形の合同条件などを使って「結論」が正しいことを示す

証明すべき結論は、BC=EDだよね？

ここで、三角形の合同を使う！

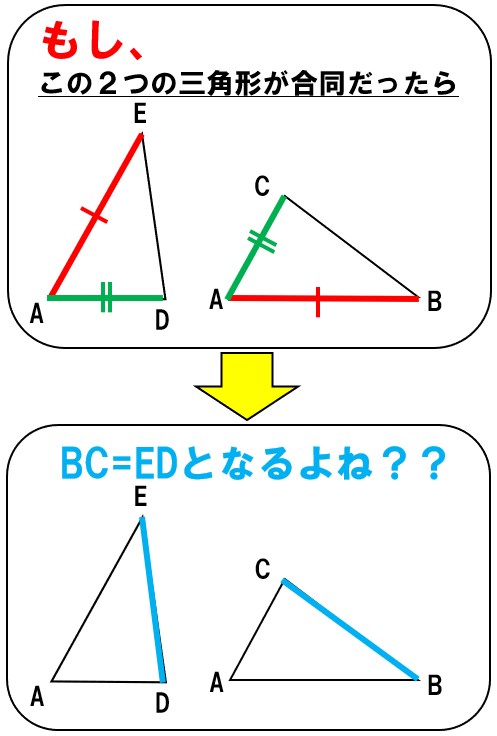
じゃあ、△ADEと△ACBが合同であることを示せばよいよね？？

ステップ２で図示したものを、もう一度見てみよう！ここに全てのヒントがある。

ここで∠Aは、△ADEと△ACBで共通する角度だよね？？

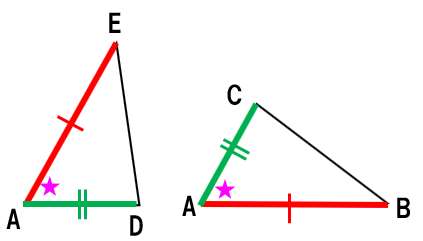
ここで三角形の合同条件を思い出して！

忘れた人はココ：三角形の合同条件

すると、２組の辺とその間の角がそれぞれ等しいので、

△ADE≡△ACBとなる。

合同な図形では、対応する辺の長さが等しいので

BC=EDである。・・・（答え）

次は、少し難しい問題に進んでね！

中２数学：証明問題（平行な２直線→三角形の合同を用いた証明）