もくじ
平行四辺形の性質を利用した証明問題のポイント
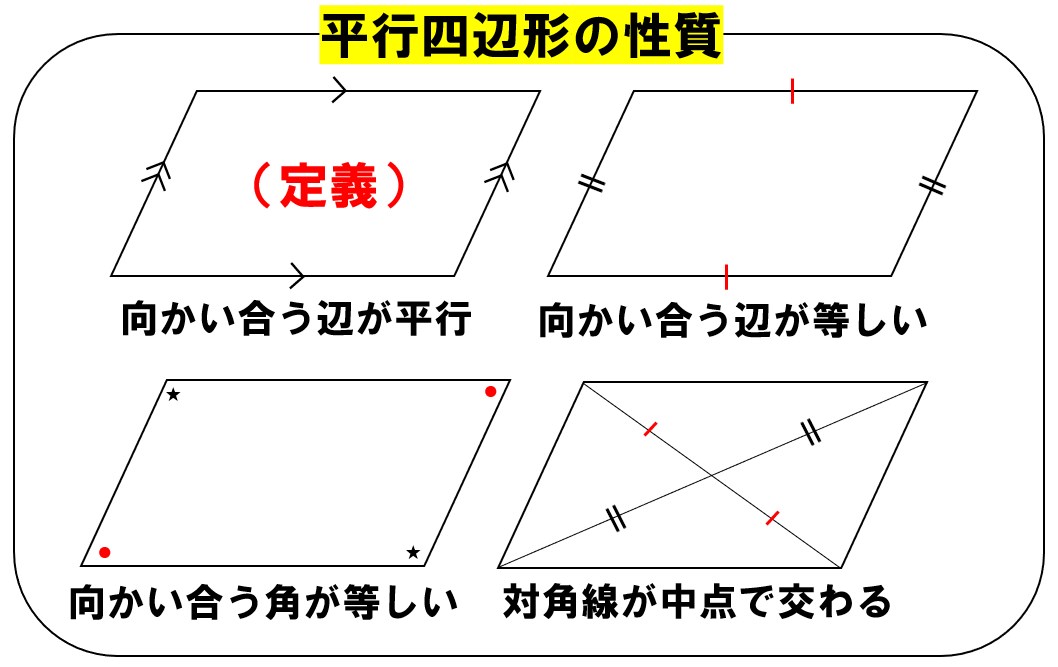
平行四辺形の性質は?
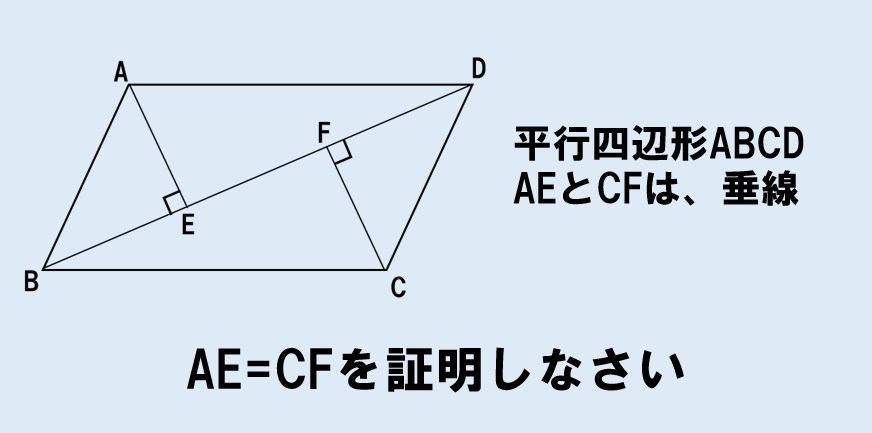
AE=CFを示すには、三角形の合同を利用する
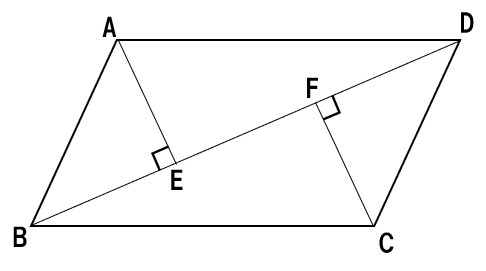
△ABEと△CDFに着目しよう!
以下の3つがポイントだ!
- 平行四辺形の性質を利用して、等しい長さを発見する
- 平行だから→錯角が使えそう!→同じ角度を発見する
- 直角三角形がある→直角三角形の合同条件が使えそう!
解き方
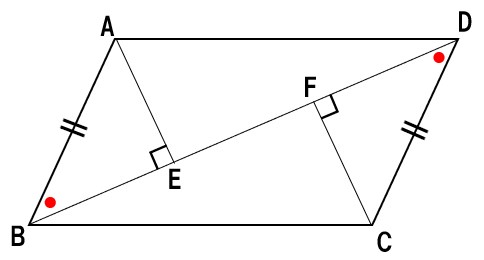
△ABEと△CDFに着目。
仮定から、∠AEB=∠CFD=90°・・・①(垂線なので)
平行四辺形は、向かい合う辺が等しいので
AB=CD・・・②
AB∥DCから、平行線の錯角は等しいので
∠ABE=∠CDF・・・③
①②③より、直角三角形の斜辺と1つの鋭角がそれぞれ等しいので、
△ABE≡△CDF
合同な三角形は、対応する辺が等しいので
AE=CF・・・(証明終わり)
理解できた?