もくじ
三角形の内接円:解法のポイント
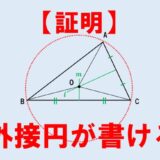
何を示せばよいか??を考えよう!
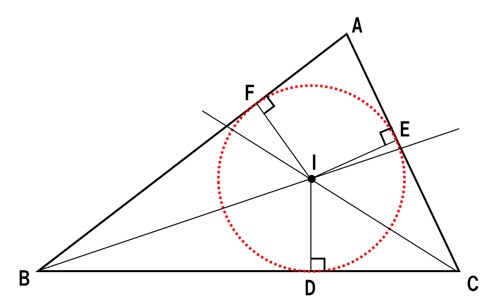
- 接する円が書けることを証明したい。
- →接する円とは、点Iを中心とした三角形の内接円
- →点Iを中心とした内接円が書けるということは、
- →ID=IE=IF(内接円の半径)を示せばよい
解き方
まず、ID=IFを示そう
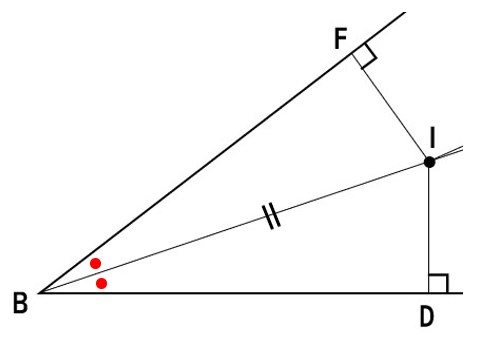
仮定より、
- ∠IBD=∠IBF (二等分線だから)
- ∠IDB=∠IFB=90°(垂線は直角だから)
- IBは共通
直角三角形の斜辺と1つの鋭角がそれぞれ等しいので、
△IBD≡△IBF
よって、
ID=IF (合同な三角形の対応する辺は等しいから)
次に、ID=IEを示そう
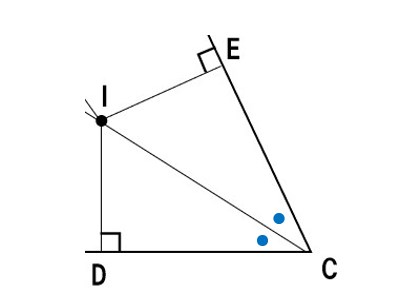
仮定より、
- ∠ICD=∠ICE (二等分線だから)
- ∠IDC=∠IEC=90°(垂線は直角だから)
- ICは共通
直角三角形の斜辺と1つの鋭角がそれぞれ等しいので、
△ICD≡△ICE
よって、
ID=IE (合同な三角形の対応する辺は等しいから)
まとめると
以上から、ID=IE=IF。
よって、点Iを中心として、辺BC,辺CA,辺ABにそれぞれ点D,点E,点Fで接する円が書ける・・・(証明終わり)
【内接円】の証明の次は【外接円】の証明問題だ!内接円問題がわかれば、そんなに難しくないので安心して!
理解できた?