もくじ
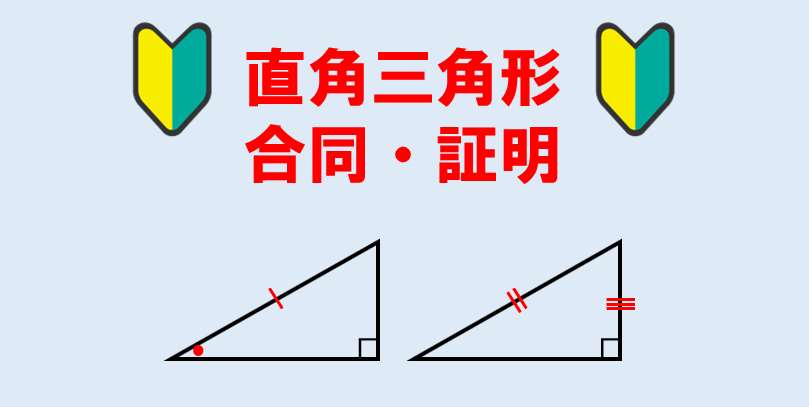
直角三角形の合同
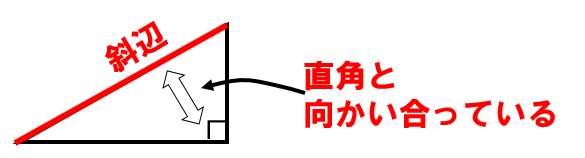
用語:斜辺
直角と向かい合っている、長い辺のことを「斜辺(しゃへん)」と呼ぶよ。
合同条件
2つの直角三角形が合同であることを示すためには、次の2つのいずれかを示せばOKだよ!
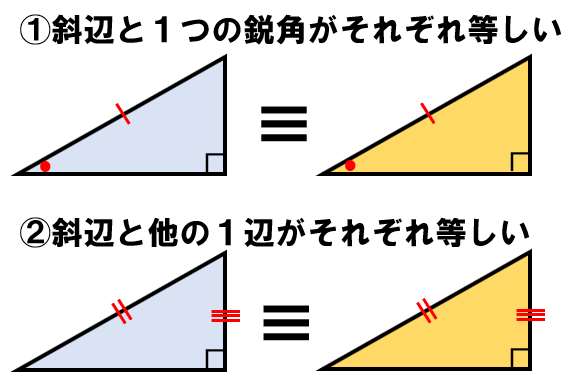
- 斜辺と1つの鋭角がそれぞれ等しい
- 斜辺と他の1辺がそれぞれ等しい
なんでこれが合同条件??
まず①の方ね。下の図のように★の角度も同じになるよね??
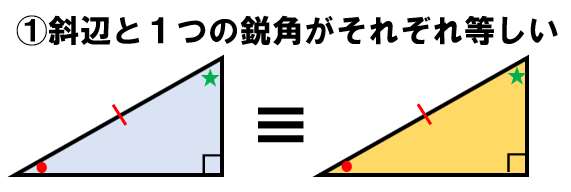
だって、★=180° -(●+90°)だから。
ってことは、通常の三角形の合同条件「1組の辺とその両端の角がそれぞれ等しい」を使えるね。
だから直角三角形の場合は、「斜辺と1つの鋭角がそれぞれ等しい」が合同条件になるんだ。
じゃあ②のほう。
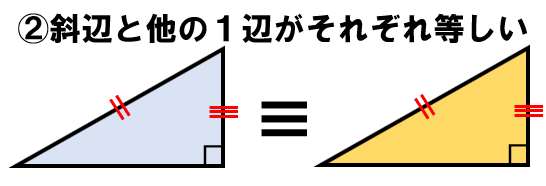
- 斜辺が等しくて
- 他の1辺も等しい
- 直角を作る
この3つを満たすと、必ず合同になるよ!やってみて!3.の直角を作るってとこがポイントね。
直角三角形の合同条件を使う証明問題
ポイント
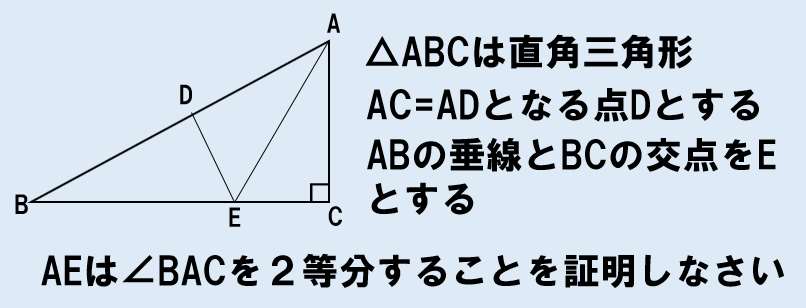
まず、わかっていること、仮定からわかることを図示してみよう。
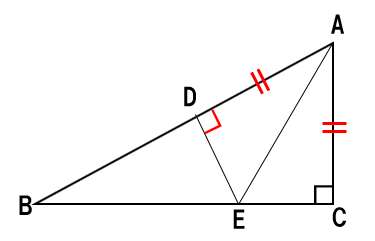
結論は「AEは∠BACを2等分する」なので、この証明をする必要があるね??
つまり、∠CAE=∠DAEを証明できればゴールなんだ!
じゃ、どうするか・・・?
今まで学んできたように、三角形の合同条件を使うのが良さそうだ!
でもね・・・もう一回図を見て。辺AEは共通なんだけど、それ以外で同じ辺や角がないんだ。。。
で、ここで気が付く必要がある。△AECと△AEDは直角三角形であることを!!
解法
仮定より
∠ACE=∠ADE=90°・・・①(直角三角形だよ!ということを示してあげる)
AC=AD・・・②
AEは共通でAE=AE・・・③
①②③より、直角三角形の斜辺と他の一辺がそれぞれ等しいので
△AEC≡△AEDである。合同な図形は対応する角が等しいので
∠CAE=∠DAE
よって、AEは∠BACを2等分する・・・(終わり)
理解できた?