二等辺三角形であることを示す証明問題だ。これも落ち着いて順番に証明していこう!
絶対できるよ!
もくじ
ポイント
二等辺三角形であることを証明するには?
二等辺三角形はこれだったよね
↓↓↓
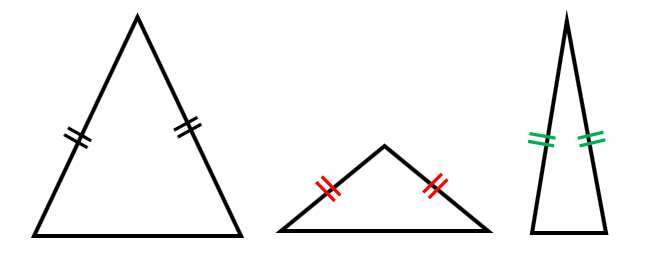
二等辺三角形の定義は、
- 2つの辺が等しい三角形を二等辺三角形という
だったね??
だから、2つの辺の長さが同じであることを示せばOK(←これがゴール)なんだ。

あとはいつもの流れ
なんとなく想像つくかもしれないけど、解法の流れは
- 三角形が合同 → だから辺の長さが同じ → 2つの辺の長さが同じ → だから二等辺三角形だ!
という流れなんだ!
解法
- ステップ1:「仮定」と「結論」を整理する
- ステップ2:「仮定」を図示する
- ステップ3:何を示せば「結論」にたどりつけるか考える
仮定と結論
仮定:∠B=∠C、AD⊥BC
結論:2つの角が等しい三角形は二等辺三角形である
仮定を図示
すでに図示してあったよ。
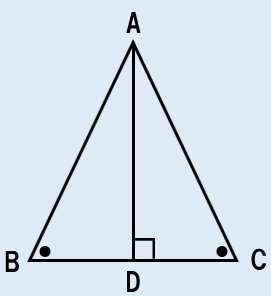
結論への筋道
二等辺三角形を示す
↓
AB=ACを示せばよい
↓
そのためには、△ABDと△ACDが合同であることを示せばよい
↓
じゃあ合同条件を考えてみよう!
という流れ。
三角形の合同を示す材料を揃えるため、もう一度図を見てみよう。
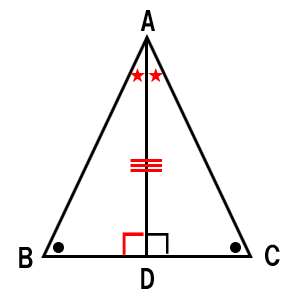
赤で示した角度や辺が、等しい部分なんだ。なぜなら、
まず、∠B=∠C・・・①
そして、ADは共通・・・②
それから、∠BDA=∠CDA=90°・・・③
三角形の内角の和は180°で、①と③から、∠BAD=∠CAD・・・④
↑↑
こういうことね!
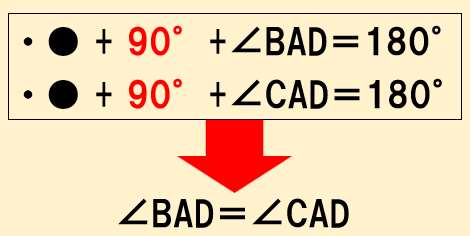
②③④から、
1組の辺とその両端の角がそれぞれ等しいので、
△ABD≡△ACD
合同な図形は対応する辺が等しいので
AB=ACとなる。
だから、2つの角が等しい三角形は二等辺三角形である・・・(終わり)
次は、ちょいムズかな??
理解できた?