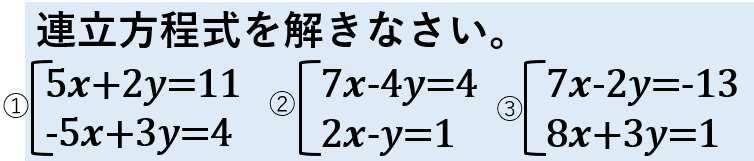
もくじ
問題
連立方程式を解きなさい。
- 5𝒙+2𝑦=11
- -5𝒙+3𝑦=4
- 7𝒙-4𝑦=4
- 2𝒙-𝑦=1
- 7𝒙-2𝑦=-13
- 8𝒙+3𝑦=1
連立方程式はそこまで難しくない!パターン化されているので、確実におさえておこう!!
解法手順
- 「x」または「y」のどちらかの係数の「絶対値」をそろえる
- 2つの式をたす(or ひく)で、文字「x」または「y」を消す
- 解く
解くための基礎知識
連立方程式を「解く」とは??
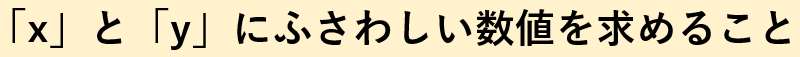
つまり、
2つの式に「x」と「y」の数値を代入したときに、
ちゃんと式が成立する→そのような「x」と「y」を求めること。
解くには「x」または「y」を消去することが必要
2つの式を
- 足し算
- 引き算
することで、「x」または「y」を消去することが必要なんだ!
その為には、
- 2つの式の「x」または「y」の係数の絶対値を揃える
- 2つの式をたし算・引き算する
たとえば、このような感じ。
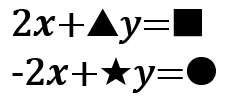
この2つの式は、「x」の絶対値が同じだね?
- 上の式の「x」の係数:2
- 下の式の「x」の係数:-2
だから、この2つの式をたし合わせて、「x」を消去するんだ!
では、具体的に解いてみよう!
解法
問題①
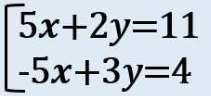
1.「x」または「y」のどちらかの係数の「絶対値」をそろえる
この問題では、xの係数の絶対値が同じだよね?だから「x」を消去することを考える!
- 上の式の「x」の係数: 5
- 下の式の「x」の係数: -5
だから、特にイジる必要はないんだ!
2.2つの式をたす(or ひく)で、文字「x」または「y」を消す
- 5𝒙+2𝑦=11
- -5𝒙+3𝑦=4
この2つの式を「たす」と、「x」が消えるね?
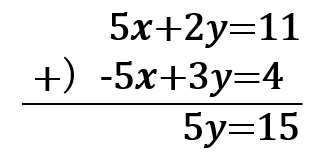
3.解く
5y=15
y=3・・・(答え)
上の式に代入して
5x+2×3=11
5x=5
x=1・・・(答え)
問題②
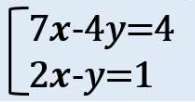
1.「x」または「y」のどちらかの係数の「絶対値」をそろえる
この問題では、「xの係数」も「yの係数」もバラバラだ。
だから簡単に「x」または「y」を消去できない!
そういう時は、どちらかの式を2倍、3倍、4倍にしてみて、
「x」または「y」の係数の絶対値を揃えるんだ!
この問題の場合、「y」の係数の方が揃えやすそうだね?
- 上の式の「y」の係数: -4
- 下の式の「y」の係数: -1
だから、下の式を4倍すると、2つの式の「yの係数の絶対値」が同じになる。
やってみよう
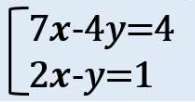
↓↓
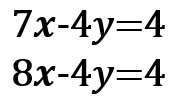
2.2つの式をたす(or ひく)で、文字「x」または「y」を消す
この2つの式を「ひく」と、「y」が消えるね?
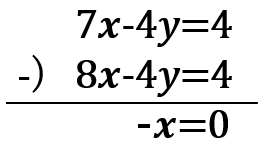
3.解く
-x=0
x=0・・・(答え)
上の式に代入して
7×0-4y=4
-4y=4
y=-1・・・(答え)
問題③
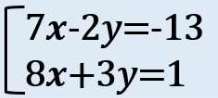
1.「x」または「y」のどちらかの係数の「絶対値」をそろえる
問題②と同じく、どちらかの式を2倍、3倍、4倍にしてみて、
「x」または「y」の係数の絶対値を揃える・・・・
で、できない!
そういう時は、上の式も下の式も2倍、3倍、4倍にしてみるんだ!
「y」の方が揃えやすそうなので、
- 上の式を3倍
- 下の式を2倍
やってみよう!
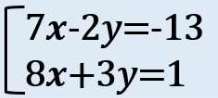
↓↓
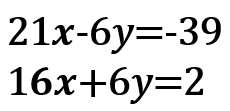
2.2つの式をたす(or ひく)で、文字「x」または「y」を消す
この2つの式を「たす」と、「y」が消えるね?
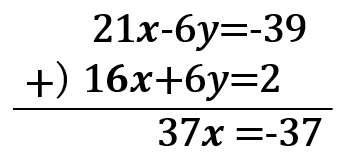
3.解く
37x=-37
x=-1・・・(答え)
上の式に代入して
21×(-1)-6y=-39
-6y=-18
y=3・・・(答え)
補足
片方の数値を求めた後、代入する式はどれでもいいよ。
「ひく」がわかりづらかったら、マイナスをかけて「たす」にしてもOK。