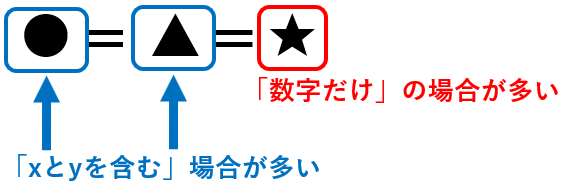
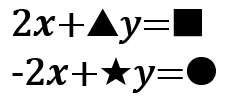問題
問題①代入法
- 𝑦-2𝒙=-3
- 2𝒙-3𝑦=1
問題②分数を含む
- 𝒙=3𝑦+2
- 𝒙/4 – 𝑦/3 =3
問題③小数を含む
- 2𝒙+5𝑦=1
- 0.4𝒙-0.3𝑦=1.5
解法手順
- 分数は分母を払う、小数は整数にする
- y=●またはx=▲として、代入して解く
解くための基礎知識
代入法
例えばこういう問題があったとしよう。これを代入法で解きなさい。
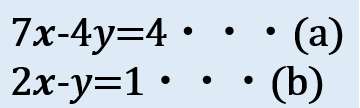
与えられた2つの式の内、1つの式を以下のように変形する。
![]() or
or
(※このケースでは(b)の式を変形した方が楽だよ!)
この式を、もう一方の与えられた式(a)に代入する。
xが解ける。
xの数値を(b)に代入して、yを解く。
分数があるとき
分数の分母を消すために、両辺に最小公倍数をかける。
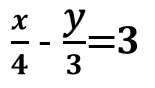
この場合、分母「4」と「3」の最小公倍数「12」を両辺にかける。
すると
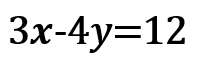
これで解けるようになるね!
小数があるとき
係数に小数があるときは、小数を消す!
具体的には、両辺を「10倍」や「100倍」する。
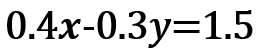
この場合、両辺を10倍すると小数が消えるね?
すると、
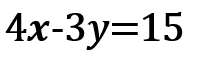
解法
問題①代入法
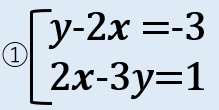
上の式を「y=●」の形にして、下の式に代入すればOKだ!
y-2x=-3
y=2x-3
これを下の式に代入すると
2x-3(2x-3)=1
2x-6x+9=1
-4x=-8
x=2・・・(答え)
x=2を上の式に代入すると
y-2×2=-3
y=1・・・(答え)
問題②分数を含む
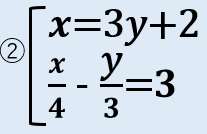
分数を消す
下の式を「12倍」すると分母を消すことができるね?
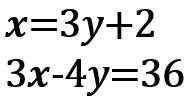
上の式
x=3y+2 を下の式に代入する。
3(3y+2)-4y=36
9y+6-4y=36
5y=30
y=6・・・(答え)
y=6を上の式に代入すると
x=3×6+2
x=20・・・(答え)
問題③小数を含む
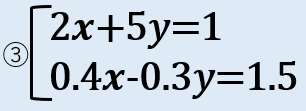
小数を消す
下の式を「10倍」すると小数を消すことができるね?
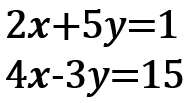
上の式を「2倍」して、「xの係数の絶対値」を揃える
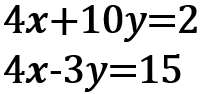
ひき算すると、
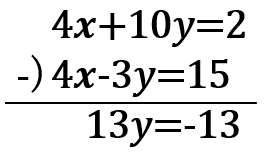
よって
y=-1・・・(答え)
上の式に代入すると、
4x+10×(-1)=2
4x-10=2
4x=12
x=3・・(答え)
理解できた?