中２数学：平行四辺形であることを証明する問題

平行四辺形であることの証明問題のポイント

「平行四辺形であることを証明しなさい」と問題文に書いてあるね？

思い出そう・・！「平行四辺形になる条件の５項目」を！！

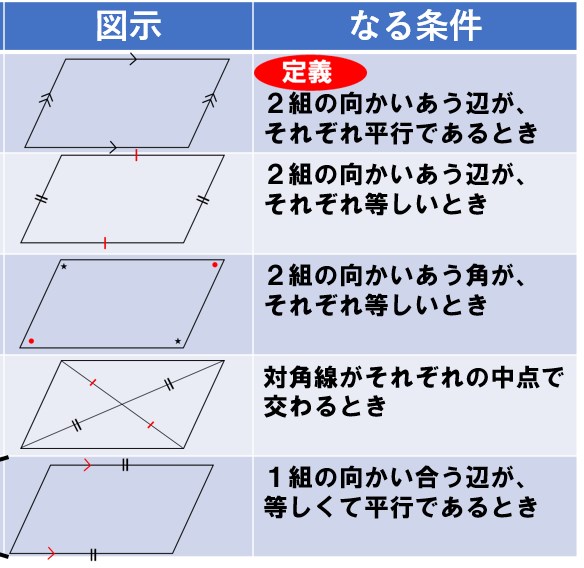
この５項目中、どれか１つでも証明できれば、平行四辺形であることが証明できるんだったね？

平行四辺形の性質や、なる条件を忘れてしまった人は、下のリンクで復習しよう！

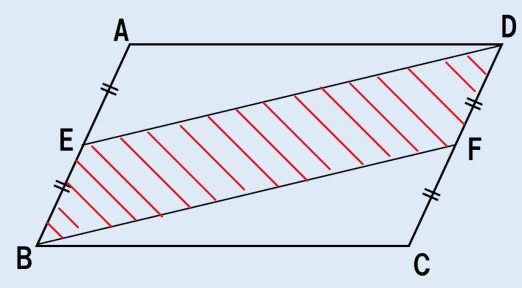
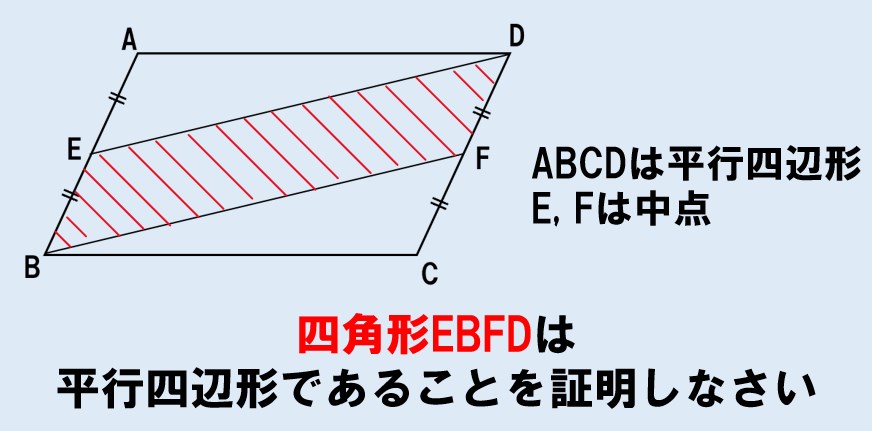
四角形EBFDを見てみると・・・

EB=DFだよね？ということは、

さらに、四角形ABCDが平行四辺形であることを考えると・・・？

ってことは、１組の向かいあう辺が、等しくて平行だよね？？

では、実際に解いてみよう！

仮定より、

AB=DC （※四角形ABCDは平行四辺形だから）

EB=1/2AB、DF=1/2DC （※中点だから）

よって、EB=DF・・・①

AB、DCは平行四辺形の向かいあう辺なので

AB∥DC

よって、EB∥DF・・・②

①②から、１組の向かいあう辺が、等しくて平行であるので、四角形EBFDは平行四辺形である。・・・（証明終わり）

中２数学：平行四辺形であるといえるか？平行四辺形かどうか確かめる問題

理解できた？