もくじ
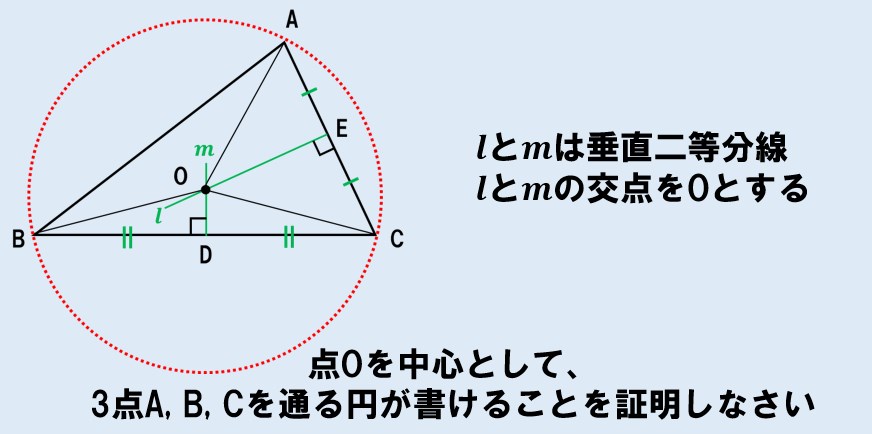
三角形の外接円:解法のポイント
何を示せばよいか??を考えよう!
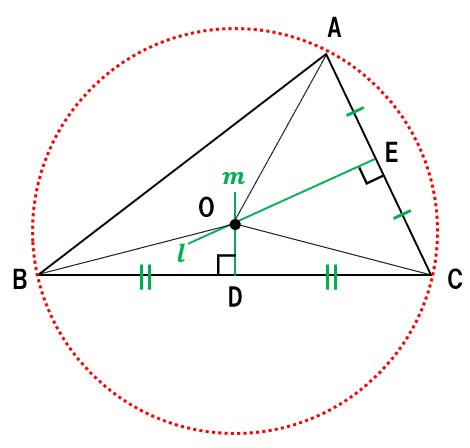
- 点Oが中心でA、B、Cを通る円
- →点Oを中心とする三角形の外接円
- →点Oを中心とした外接円が書けるということは、
- →OA=OB=OC(外接円の半径)を示せばよい
解き方
まず、OA=OCを示そう
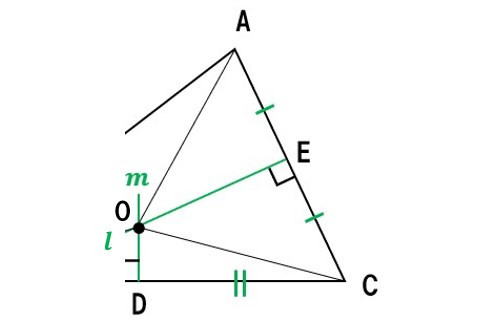
仮定より、
- AE=CE (lは垂直二等分線だから)
- ∠OEA=∠OEC(lは垂直二等分線だから)
- OEは共通
よって、2組の辺とその間の角がそれぞれ等しいので、
△OAE≡△OCE
よって、
OA=OC (合同な三角形の対応する辺は等しいから)
次に、OB=OCを示そう
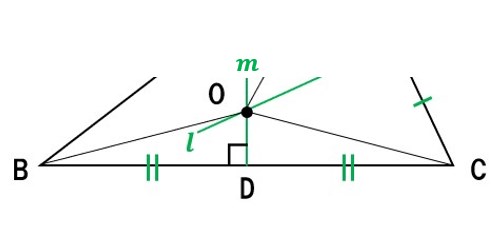
仮定より、
- BD=CD (mは垂直二等分線だから)
- ∠ODB=∠ODC(lは垂直二等分線だから)
- ODは共通
よって、2組の辺とその間の角がそれぞれ等しいので、
△OBD≡△OCD
よって、
OB=OC (合同な三角形の対応する辺は等しいから)
まとめると
以上から、OA=OB=OC。
よって、点Oを中心として、3点A, B, Cを通る円が書ける・・・(証明終わり)
次は平行四辺形問題!平行四辺形の性質を利用した【証明問題】だよ!
理解できた?