もくじ
問題
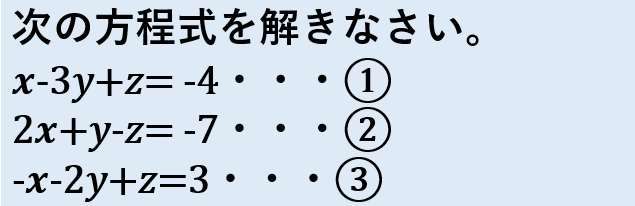
次の方程式を解きなさい。
x–3𝑦+𝑧= -4・・・①
2x+𝑦–𝑧= ‐1・・・②
–x–2𝑦+𝑧=3・・・③
基礎知識とポイント
今まで解いてきた連立方程式は「x」と「y」の2つの文字だったよね?
でも今回は「x」と「y」と「z」の3つの文字がある!
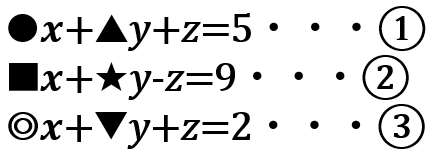
これだと、普通に解けないよね?
そういう時は、文字を1つ消すんだ!!
手順は、
- 消しやすい文字を見つける
- 「消しやすい文字を消した式」を2つ作る
- 解く
消しやすい文字を見つける
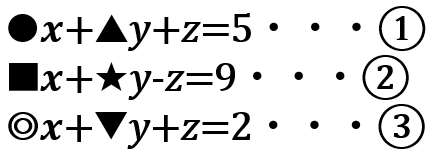
この場合だったら、「z」が消しやすいよね?
なぜなら
- ①+②で「z」が消える
- ②+③で「z」が消える
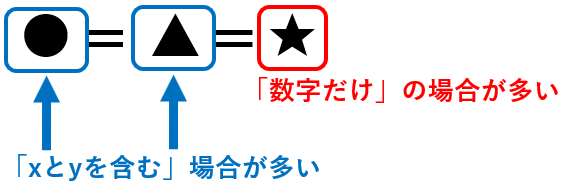
こういう風に、「係数が揃えやすい文字を消す」のが鉄則なんだ!
では、これだったらどう?どの文字が消しやすいかわかるかな??
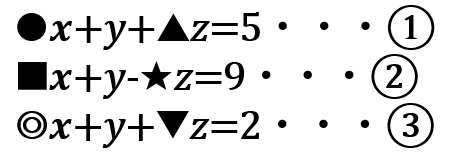
・・・
この場合は、「y」が消しやすいね。yの係数は「1」で揃っているからね!
こうやって、消しやすい文字を見分けるのが第一ステップです!
「消しやすい文字を消した式」を2つ作る
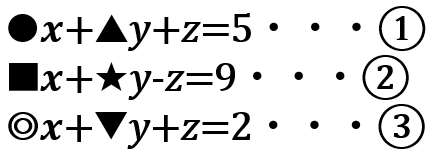
このケースだったら、「z」を消すのが楽なので、
①+②で
![]()
②+③で
![]()
あとは、これを普通の連立方程式として解けばいいんだ!
解法

さあ順番にやっていこう!
消しやすい文字を見つける
「z」を消すのが一番楽だ。だって、「z」の係数が揃っているから。
zを消そう!!
「消しやすい文字を消した式」を2つ作る

①~③の式で、「z」を消した式を2つ作るんだ。
どの2つを選ぶか?その組み合わせは自由!
今回は、
- ①+②で「z」を消す
- ②+③で「z」を消す
すると
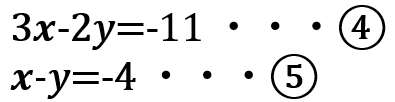
解く
④と⑤の連立方程式を解くと
x=-3、y=1・・・(答え)
①に代入すると
z=2・・・(答え)
理解できた?