もくじ
そもそもグラフを書く意味は??
グラフってなんやねん!?って話。
簡単に言うなら、
xとyを満たす「点」の集まりと言えるね。
例えば、
y=x という一次方程式があったとしよう。
これを満たす(x,y)の組み合わせは、
(x,y)=(1,1),(2,2),(3,3)とか、
(x,y)=(-1,-1),(-2,-2),(-3,-3)とか、さらには
(x,y)=(0.1,0.1),(2.4,2.4),(3.56,3.56)とか、
無限にあるわけだ!!
だから、パッと見でxとyの値をイメージできるようにしたのがグラフなんだ。
y=x のグラフはこんな感じになるんだ。
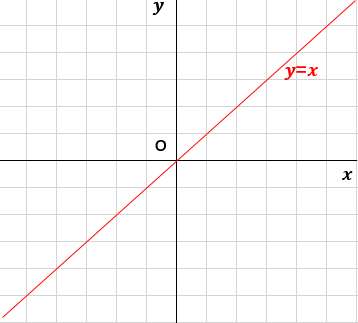
方眼の1目盛りが1を表すよ。
さっき言った
(x,y)=(1,1),(2,2),(3,3),(-1,-1),(-2,-2),(-3,-3),(0.1,0.1),(2.4,2.4),(3.56,3.56)
これらは全て、y=x の赤い線状にある点だよね。xとyの数値に当てはまる点をを集めたのがグラフなんだ。
ポイント
切片と傾きを確実に理解しよう!!
グラフを書ために絶対知っておくべきことは「切片」と「傾き」だよ!

グラフの書き方を理解しよう!
例として、次の一次方程式のグラフを書く練習をしてみよう!
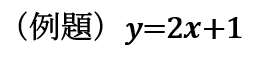
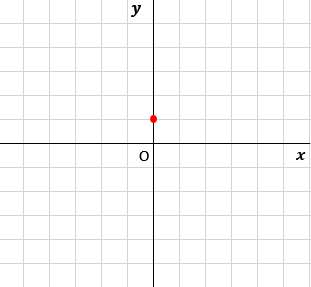
ステップ1:切片をy軸上にプロットする
切片は、「1」だね?グラフの1目盛り分は「1」なので、
グラフのy軸上に次のようにプロット(=点を打つという意味)するよ。
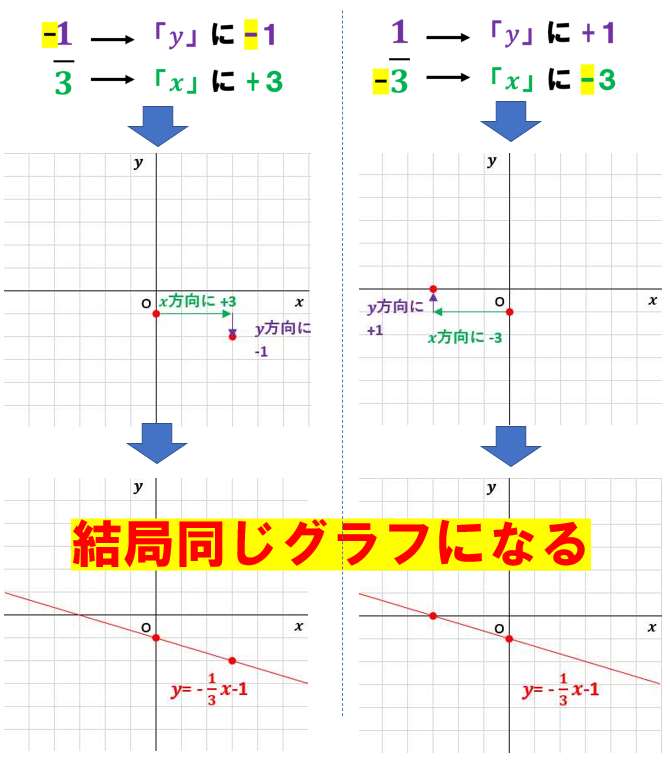
ステップ2:傾きを分数にする
傾きを分数にする。(意味はわからなくてもまずはやってみて欲しい!)

ステップ3:もう1点だけグラフにプロットする
ここがポイントだ!
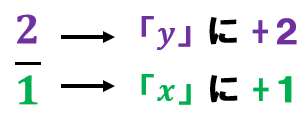
ステップ1でプロットしたy軸上の点から、進むんだ。
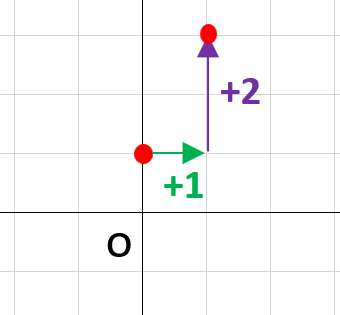
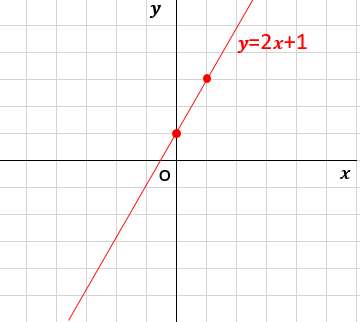
ステップ4:グラフを完成させる
プロットした2点を結んで完成
補足
なんで切片はy軸にプロットするの??x軸でない理由は??
実は、切片の値というのは、x=0の時のyの値なんだ!
ほらこれを思い出して
↓↓↓

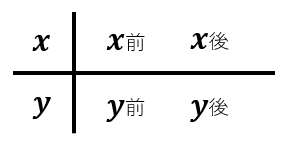
x=0を入れたら、切片▲だけが残るよね?
つまり切片が表す座標は
(x,y)=(0,▲)なんだ!!
だから、x=0 つまり、y軸上の点になるわけ!
練習問題