もくじ
ポイント
今回の問題は、ちょっといつもと違う!
わかれば簡単なんだけど、いつものように三角形の合同条件を使って示す問題ではないんだ。
考え方を整理しておくね!!
三角形の合同条件を使うと・・?
まず、FB=FCを証明するのがゴールだとわかるよね?
↓↓

いつもなら、こう考えるんじゃないかな・・・?
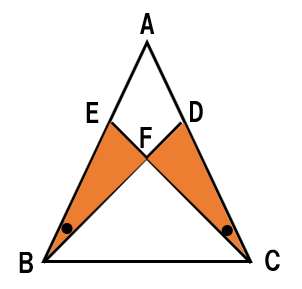
△EBFと△DCFが合同を示す → FB=FC
でもね・・・
この考え方は、今回はダメ!!

なぜなら、
与えられた仮定だけでは、合同が示せないから。
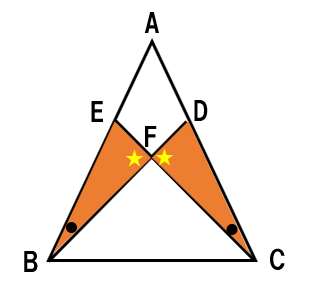
確かに黄色の★は同じ(対頂角)だけど、そこで終わり。(錯角や同位角もないね?)
仮定の条件では、これ以上「同じ長さの辺」や「同じ大きさの角度」を見つけることができない。
△EBFと△DCFが合同を示すことは不可能なんだ!!
二等辺三角形の条件を使う
じゃあどうする・・・?路線変更!
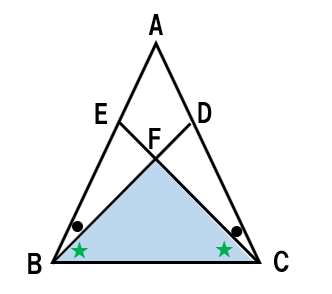
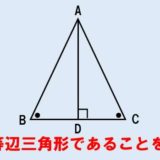
△FBCに注目!これは二等辺三角形なんだ。
なぜなら△ABCが二等辺三角形だから
∠ABC=∠ACB
そして
●は等しいので、★も等しくなる
(※詳しくは、下の解法をみてね!)
△FBCが二等辺三角形だとわかったので、FB=FCとなる。
二等辺三角形であることを証明するには?
それから、もう1つポイント。
ある三角形が二等辺三角形であることを証明するには、1or2のどちらかを示せばOKなんだ。
- 2つの辺が等しい
- 2つの角が等しい
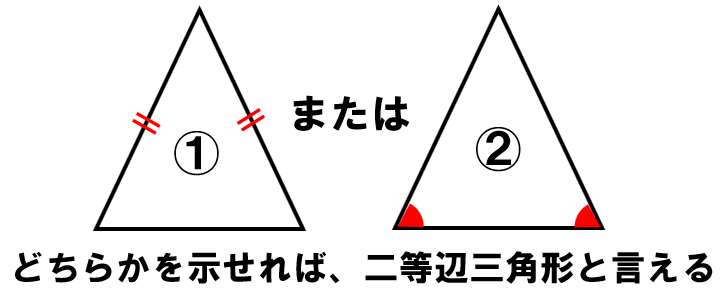
今回の問題は、②で示すパターンだね!
解法
じゃあ、実際の解法の流れを説明していくよ。
- ステップ1:「仮定」と「結論」を整理する
- ステップ2:「仮定」を図示する
- ステップ3:何を示せば「結論」にたどりつけるか考える
仮定と結論
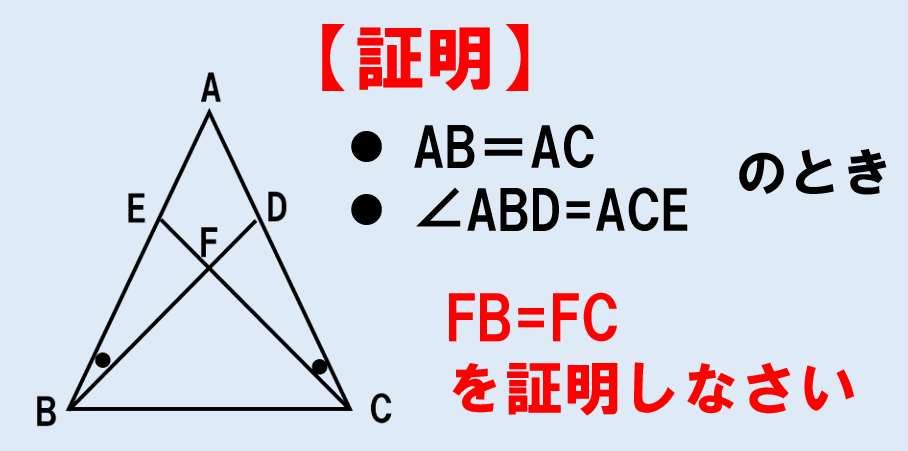
仮定:AB=AC、∠ABD=ACE
結論:FB=FC
仮定(+わかったこと)を図示
AB=ACということは、△ABCは二等辺三角形である。
二等辺三角形の底角は等しいから、以下のように図示できる。
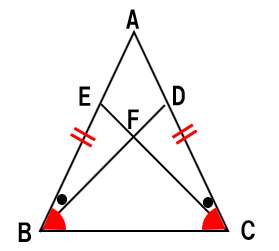
結論への筋道
∠ABC=∠ACB・・・①
仮定から、∠ABD=∠ACE・・・②
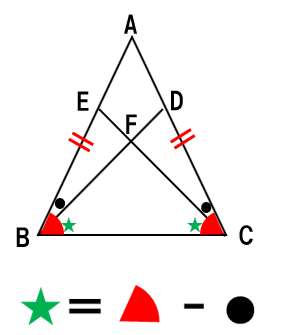
でね、上の図のように、★同士は等しいことを示すんだけど、これを式で表さないといけない。
みんなここに、ちょっと抵抗があるみたいだね。
「★イコール赤の扇マイナス●」という式を、左の底角と右の底角で、それぞれ作ってみよう。
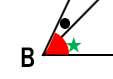
∠FBC=∠ABC – ∠ABD

∠FCB=∠ACB – ∠ACE
整理すると
- ∠FBC=∠ABC – ∠ABD
- ∠FCB=∠ACB – ∠ACE
で、∠FBC=∠FCBを示したいわけだよね??
①②から、
∠FBC=∠ABC – ∠ABD=∠ACB – ∠ACE = ∠FCB
よって、
∠FBC=∠FCB
これわかる・・・?こういうこと
↓↓
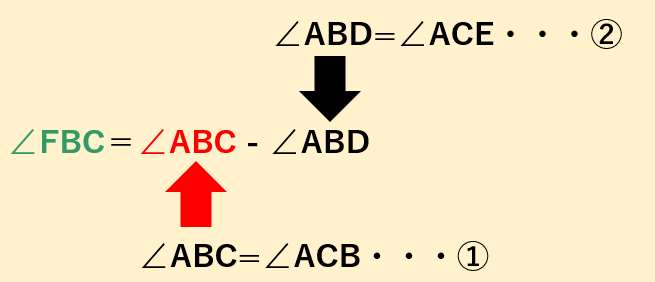
すると、∠FBCは

これって、∠FCBと同じじゃん!ってことで、∠FBC=∠FCBになるわけ。
で、2つの角が等しいので、△FBCは二等辺三角形である。
よって、FB=FC・・・(終わり)
ちょっと長かったね?次はガラッと変わって「逆」を学ぶよ!とても簡単なので息抜きだ!