もくじ
二等辺三角形の性質
二等辺三角形とは、
- 定義:2つの辺が等しい三角形
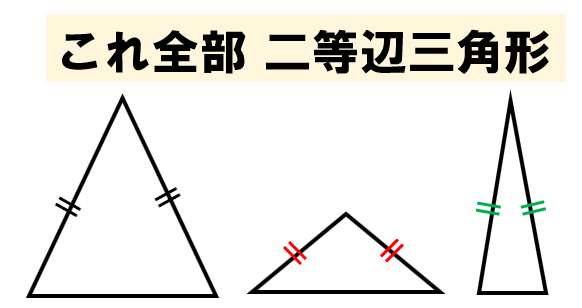
三角形を見て、辺の長さが2つ同じであれば、それは二等辺三角形だよ!
二等辺三角形の用語
等しい2つの辺が屋根のようになっている状態で考えるよ!
このとき、3つの呼び名を覚えて欲しい!
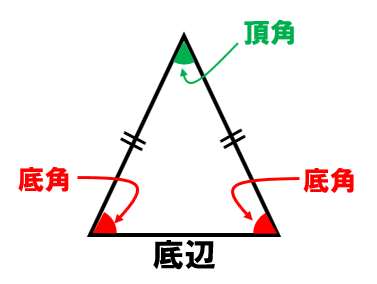
- 底辺:下の辺(これは知ってるね)
- 底角:底辺の両端にある角
- 頂角:頂上にある角
丸暗記すること!
二等辺三角形で覚えておくべきこと

- 2つの辺の長さが等しい
- 2つの底角が等しい
まぁ、見たまんまなんだけどね。きちんと覚えておこうね!!
直角二等辺三角形
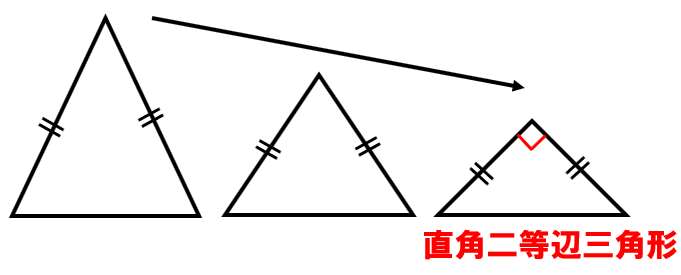
二等辺三角形を押さえつけて、背を小さくしていくと・・・・
あるところまで小さくすると、頂角が90°になる。
この二等辺三角形を、直角二等辺三角形と呼ぶよ。
二等辺三角形の証明問題
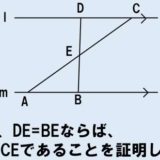
それじゃあ練習問題を1問解いてみようね。二等辺三角形を含む証明問題だよ。

解法のステップ
- ステップ1:「仮定」と「結論」を整理する
- ステップ2:「仮定」を図示する
- ステップ3:何を示せば「結論」にたどりつけるか考える
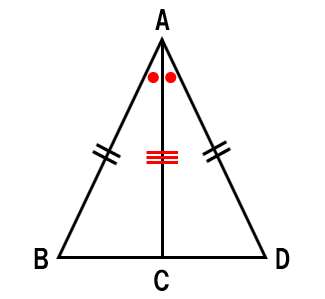
仮定と結論の整理
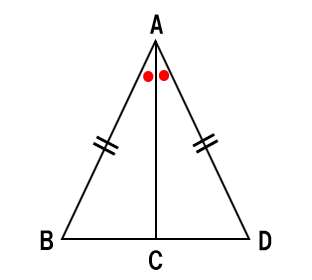
- 仮定:AB=AD、∠Aは二等分されている
- 結論:線分ACは底辺BDを垂直に2等分する
仮定を図示
結論への筋道
線分ACは底辺BDを垂直に2等分することを証明する必要があるね
ポイントは垂直に2等分というところ。
ただの2等分ではなく、垂直じゃないとダメなんだ。
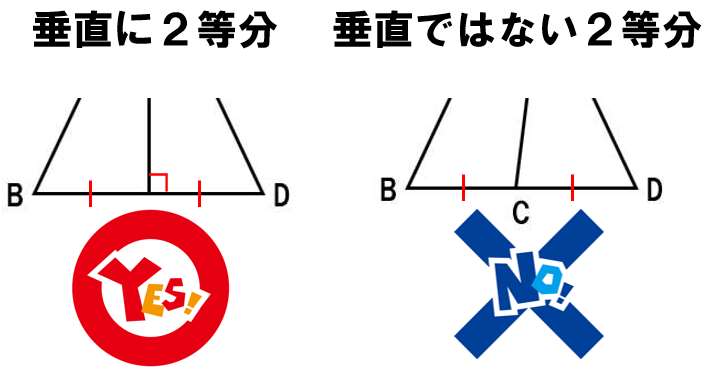
だから示すべきは、この2つなんだ。
- BC=DC
- ∠BCA=∠DCA=90°
じゃあ、この結論を示すためには、どうしたらいいかを考えてみよう!
先に答え(証明の筋道)を言っちゃうよ!
- 2つの三角形が合同
- だからBC=DC
- ∠BCA=∠DCA=90°
なぜこう考えるか?みていこうね。
まず、BC=DCを示す
まず、三角形が2つあるので、三角形の合同条件を使えば良さそうだよね。
線分ACは、2つの三角形(△ABCと△ADC)で共通だよ。
分かっていることを整理すると
- AB=AD・・・①
- ACは共通・・・②
- ∠BAC=∠DAC・・・③
よって、①~③より、2組の辺とその間の角がそれぞれ等しいので
△ABC≡△ADC
合同な図形では対応する辺が等しいので
BC=DC(←結論の1つ目が示されたよ!)
次に、∠BCA=∠DCA=90°を示す
合同な図形では対応する角が等しいので
∠BCA=∠DCA
さらに∠BCA +∠DCA=180°(一直線上なので)なので、
∠BCA=∠DCA=90°(←結論の2つ目が示されたよ!)
よって、線分ACは、底辺BDを垂直に2等分する・・・(終わり)
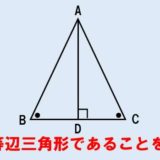
次の問題は、二等辺三角形の証明問題だよ!
理解できた?