もくじ
ポイント
長方形・ひし形・正方形の「定義」
これは暗記してね!!
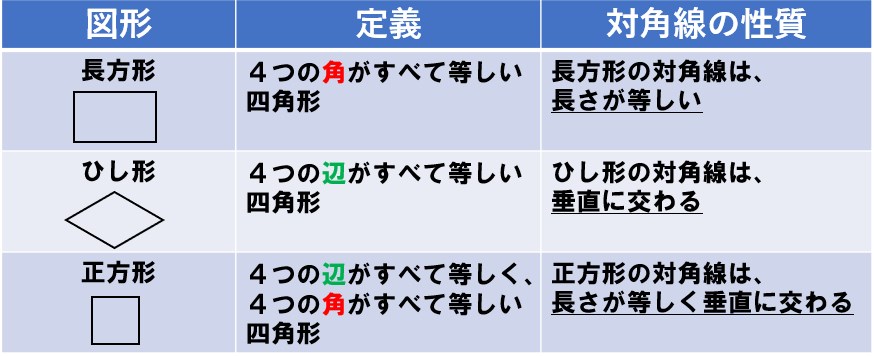
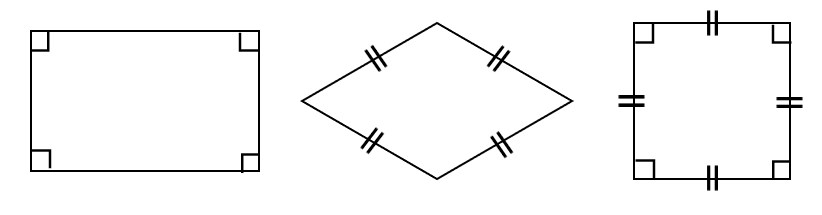
長方形・ひし形・正方形の定義
長方形:4つの角がすべて等しい四角形
ひし形:4つの辺がすべて等しい四角形
正方形:4つの辺がすべて等しく、4つの角がすべて等しい四角形
例えば、問題文に「四角形ABCDは長方形です」と書かれていたら、4つの角がすべて等しい。ということを使ってOK!
長方形・ひし形・正方形の「対角線の性質」
対角線の性質
長方形の対角線は、長さが等しい
ひし形の対角線は、垂直に交わる
正方形の対角線は、長さが等しく垂直に交わる
四角形が「長方形・ひし形・正方形」であることを証明するには?
- 四角形が長方形であることを証明するには?
→長方形の定義にあてはまることを示す。 - 四角形がひし形であることを証明するには?
→長方形の定義にあてはまることを示す。 - 四角形が正方形であることを証明するには?
→長方形の定義にあてはまることを示す。
【例題】どんな四角形になる?
平行四辺形ABCDに、次の条件を加えると、どんな図形になりますか?(対角線の交点をOとする)
(1)OA=OB
(2)∠OAB+∠OBA=90°
解く前に
ABCDは平行四辺形であることが問題文に書いてあるね。
じゃあ、平行四辺形の性質4つを思い出そう!これだね↓↓
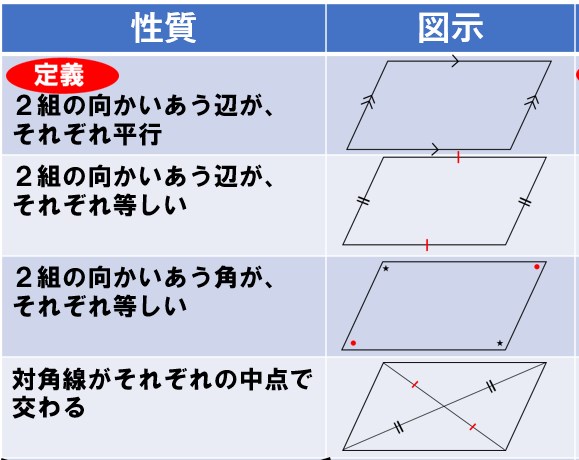
もし忘れているなら、このページで復習!
 中2数学:平行四辺形の「性質」と平行四辺形に「なる条件」の違い
中2数学:平行四辺形の「性質」と平行四辺形に「なる条件」の違い
(1)OA=OB

OAやOBは対角線に関する長さなので、まずは平行四辺形の性質4番目を図示してみよう。
- 平行四辺形の性質:対角線がそれぞれの中点で交わる。
つまり、OA=OC、OB=ODとなる。
ここに、OA=OBの条件を加えると
OA=OC=OB=ODとなる。
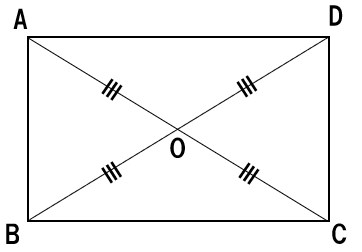
対角線の長さが等しいので、ABCDは長方形となる。
(2)∠OAB+∠OBA=90°

角度が与えられている→新たにわかる角度が無いか確認!
△ABOに着目すると、三角形の内角の和は180°なので
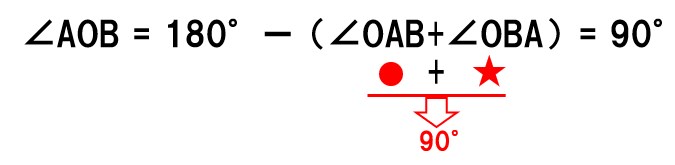
∠AOB=90°となる。
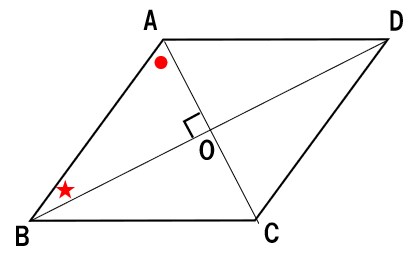
対角線が垂直に交わるので、ABCDはひし形となる。
次は、平行線と面積!
理解できた?