問題
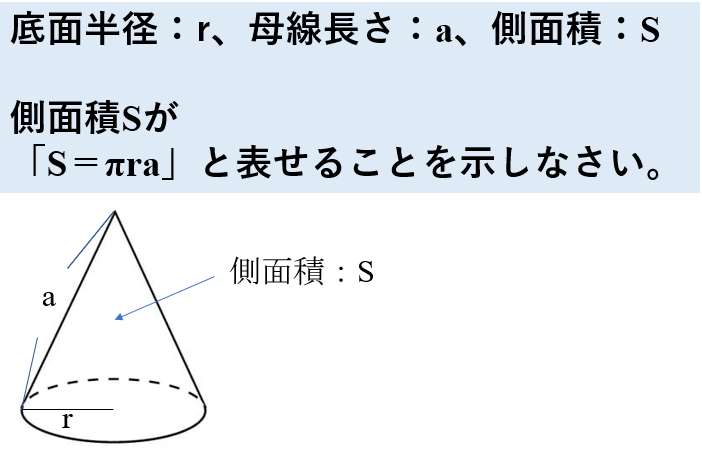
底面半径：r、母線長さ：a、側面積：S
側面積Sが「S＝πra」と表せることを示しなさい。
これは、難しいかもしれない！
順番に解いていこう。
解法手順
- 展開図を書く
- 側面積を求める（式①）
- もう１つの式を立てる（式②）
- 式①と式②により、答えを導く
解くための基礎知識
円錐の展開図
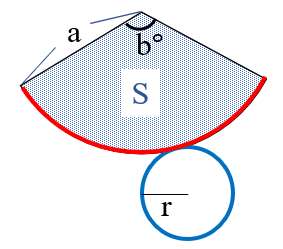
「赤の長さ」と「青の長さ」は等しい
解法
展開図を書く
側面積を求めるために、まずは「展開図」を書いてみよう。
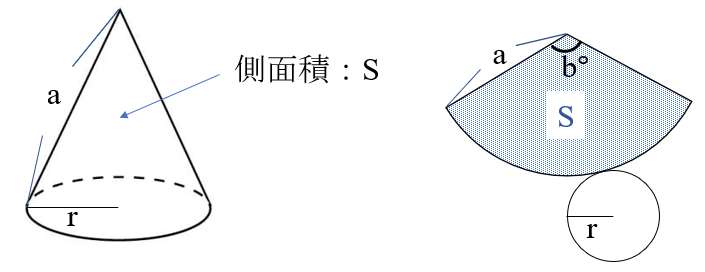
扇形の中心角は、わからないので「b°」としておく。
側面積を求める→（式①となる）
問題文を見ると、
側面積「S」を、文字を用いて表すように言われているよね？？
だから、まずは言われた通り、側面積「S」を求めてみよう！
展開図の扇形の角度は「b°」とおいたので、側面積Sは、
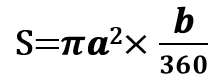・・・式①と表すことにする
もう１つの式を立てる→（式②となる）
そして、ここがつまづきやすいポイントかな？
まず整理する為、
問題文で求められている「S」の式と、今求めた「S（式①）」を比べてみよう
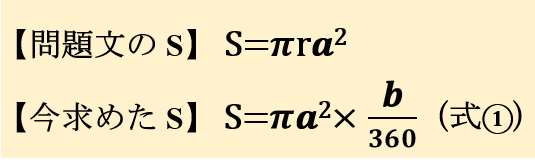
【今求めたS】を、どうすれば【問題文のSの式】に近づけられるか考えるんだ。
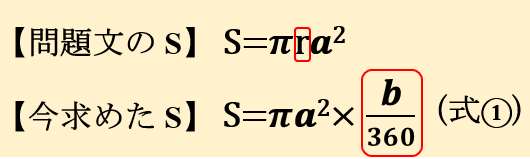
すると、【今求めたS】に対して
- r を付け加えたい
- b/360 を消したい
↑↑これが必要なんだ！
だから、
「b」や「r」を用いた、もう１つの式を立てることを目指す必要があるんだ！
なにか、もう１つ式を立てられないかな・・・？？？
と考えてみて！
そこで注目するのが、
「赤の長さ」と「青の長さ」は等しいこと。
これで、もう１つ式を立てられるんだ。長さが等しいことを利用して、
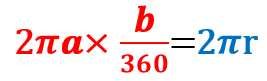・・・式②と表すことにする
式①と式②により、答えを導く
ここまでを整理してみよう
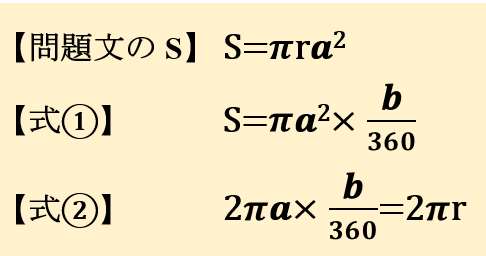
【式①】と【式②】を用いて、【問題文のS】に変形するにはどうすればよいか考える
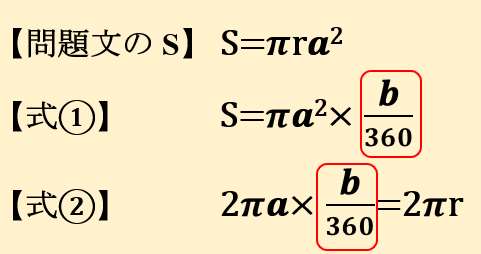
すると、
消したい「b/360」が【式②】にも表れていることがわかる！
だから【式②】を変形して、【式①】に代入すればいいんだ！！！
【式②】を変形すると
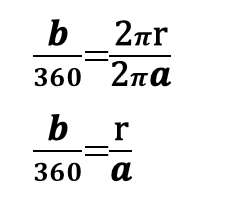
この結果を【式①】に代入すると
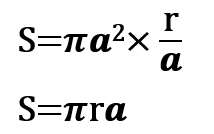・・・（答え）
補足
なし
理解できた？
