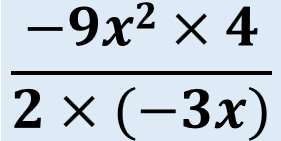中２数学：文字式の利用（２ケタの正数を文字式を使って説明）

問題

2ケタの正の整数に、その整数の十の位から一の位の数をひいた差を加えると、11の倍数になる。その理由を説明しなさい。

中二数学で、避けて通れない問題。この分野、苦手意識を持っている人も多いかも・・・。

でも大丈夫！１つずつ、数字で置き換えて、具体的にイメージすることで、理解しやすくなるよ！

解法手順

文章を整理する
具体的数字でイメージする
文字式を使って、問題文の言うとおりに計算する
ゴールの形に

解くための基礎知識

２ケタの正の整数は、

十の位を a
一の位を b

とすると、

10a+bであらわすことができる。

なんでって？？？

たとえば、「24」は

十の位は 2
一の位は 4

(10×2)+4 で表すことができるでしょ？？だからだよ。

解法

①文章を整理する

まずね・・・、

文章が長くてわかりづらい！！何を言っているか、すぐに理解できないよね・・？

だから、整理すべきなんだ！第一ステップとして必ずやった方が良いよ！

文章を区切って
箇条書きにする

この２つをやってみよう！するとこんな感じに

どうだろう？

はじめよりも、かなりわかりやすくなったよね？

問題を要約すると

「十の位の数」と「一の位の数」を引き算して、それを2ケタの正数に足す。すると11の倍数になるのはなんで～？？

ってことだよ。

②具体的数字でイメージする

文章が理解できたら、次は具体的な数字を当てはめてみよう。

なぜなら

理解を深めるため
解き方のヒントになるため

２ケタの正数なら何でもいいので、たとえば、

を考えてみよう。

（別に37じゃなくても何でもいいんだよ！例としてね）

２ケタの正の整数 → 37
十の位から一の位の数をひいた差 → (3-7)

だから、この２つの数をたしあわせると、

37+(3-7)=33

33になる。これは確かに「11の倍数」だよね？？

問題の通り、11の倍数になることがわかったね。

具体的に問題＆解法のイメージができてきたかな？？

（★慣れてきたら、この「ステップ2」は省略してもOKです。）

③文字式を使って、問題文の言うとおりに計算する

２ケタの正の整数を

十の位　→　a
一の位　→　b

すると、この整数は

10a+bで表すことができる。

そして、素直に問題文の言う通りやってみることだ！

（10a+b)+(a-b)

=10a+a+b-b

=11a

④ゴールの形に

もう答えは出たね？

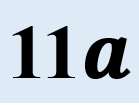
この形は、

「11×●」なので、11の倍数になるわけ！

理解できた？

問題