これまでみんなは、三角形の角や平行、三角形・四角形の角度の求め方を学んできたよね??
次は、合同(ごうどう)について学習していくよ!聞きなれない言葉だけど、1つずつ進んでいこう。
もくじ
合同とは?
合同は「合わせると同じ」ということだ!
2つの図形があって、その2つの図形を重ね合わせると全く同じのとき、2つの図形を合同と呼ぶよ!
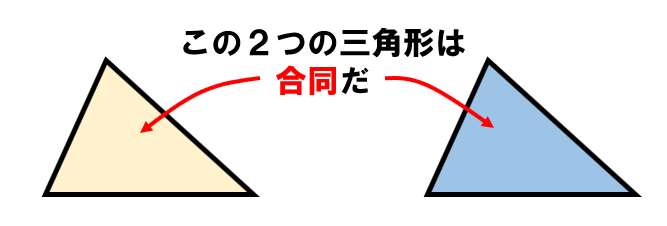
合同の表し方(記号)
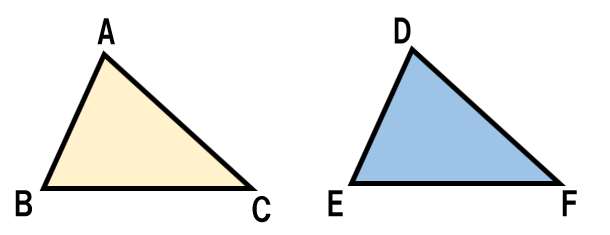
上の2つの三角形が合同のとき、
△ABC≡△DEF と表すよ。合同の記号は「≡」だよ!!
| OKな書き方 | NGな書き方(赤字がNGな部分) |
|---|---|
| △ABC≡△DEF | △ABC≡△DFE |
| 辺ACに対応するのは、辺DFです。 | 辺ACに対応するのは、辺FDです。 |
合同な四角形「対応する辺や角」の問題
合同な2つの四角形がある。
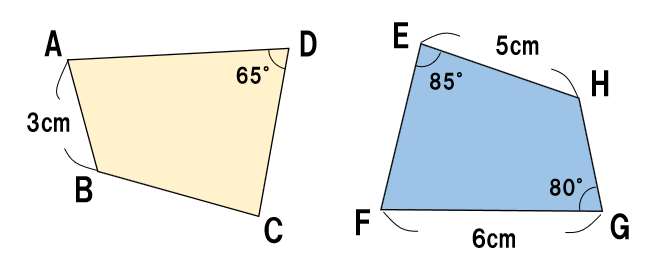
(1)2つの四角形の合同を記号を用いて表しなさい
(2)頂点Aに対応する点はどれ?
(3)辺BCに対応する辺はどこ?
(4)辺HGの長さは?
(5)∠Fの大きさは
(6)【ちょい難】∠Bの大きさは?
(1)2つの四角形の合同を記号を用いて表しなさい
頂点の対応に気を付けて、慎重にね!
四角形ABCD≡四角形GHEF・・・(答え)
(2)頂点Aに対応する点は?
頂点G・・・(答え)
(3)辺BCに対応する辺は?
辺の順番に気を付けて、辺HE・・・(答え)
辺EHではダメだからね!
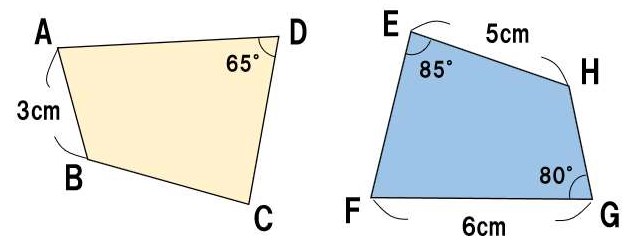
(4)辺HGの長さは?
辺HGに対応するのは、辺BAだから、3cm・・・(答え)
(5)∠Fの大きさは
∠Fに対応するのは∠Dだから、65°・・・(答え)
(6)【ちょい難】∠Bの大きさは?
まず、2つの四角形は合同なので、∠Aと∠Cがわかるよね?
このように↓↓
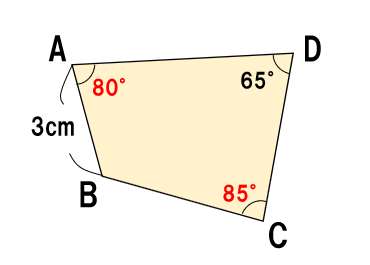
四角形ABCDの内角の和は360°なので、
∠B=360° -(80°+65°+85°)=130°・・・(答え)
三角形の合同条件
次は、三角形の合同条件を見ていこう!
三角形の合同条件3つ
まずはイメージしてみよう!合同条件は、この3つだ。
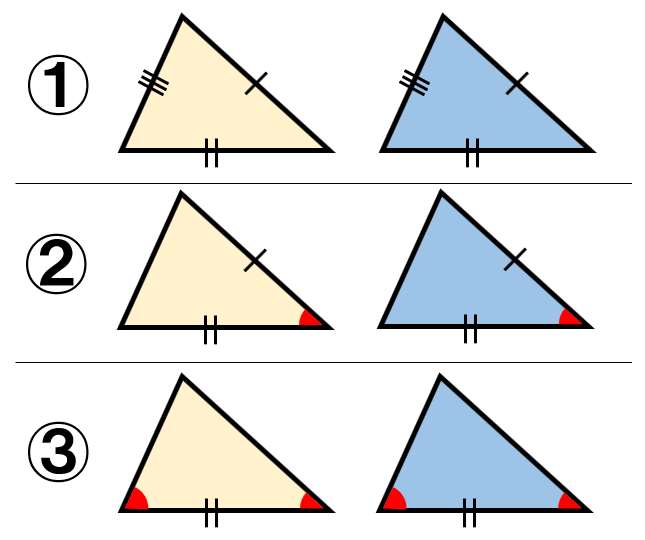
三角形の合同条件①
- 3組の辺がそれぞれ等しい。
3つの辺が、ぜ~んぶ同じ長さだったら全く同じ三角形になるよね??
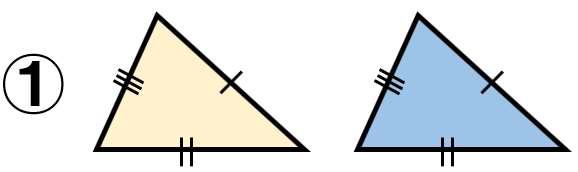
三角形の合同条件②
- 2組の辺とその間の角がそれぞれ等しい。
2つの辺の長さが同じで、挟まれた間の角も同じだったら、残りの1辺も長さが勝手に決まるね。
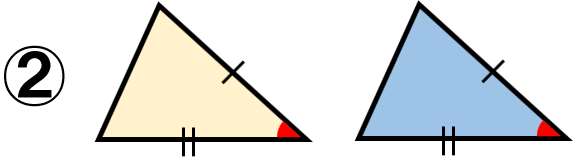
三角形の合同条件③
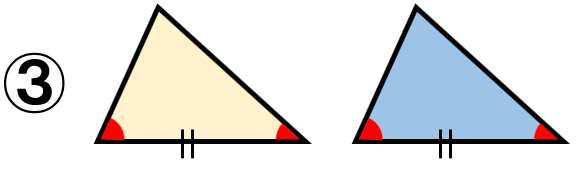
- 1組の辺とその両端の角がそれぞれ等しい。
1つの辺の長さが同じで、両端の角が同じなら、のこり2つの辺も同じ長さになるよ!
合同な三角形を見つける問題
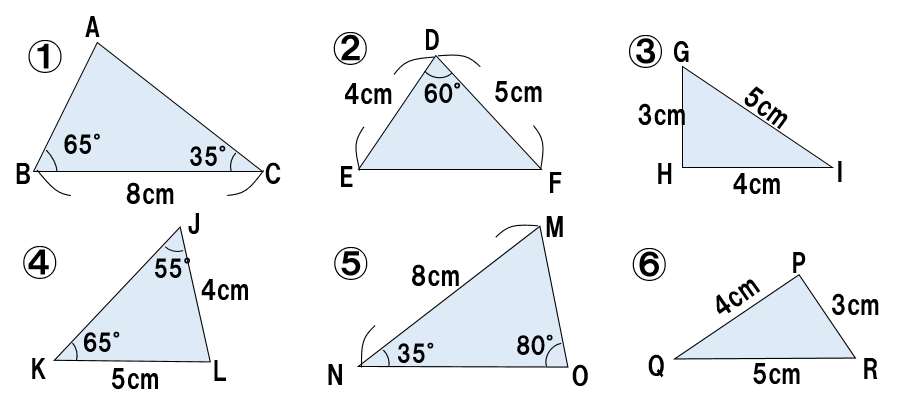
合同な三角形の組に分け、記号≡を用いて表しなさい。
また、合同の条件を言いなさい。
ポイント
わかる角度を書き込む
求めることができる角度を書き込んでしまおう!!めんどくさがらず、これをやる方が実は早く解けるんだ!
こうすることで、合同の三角形が見つけやすくなるからね☆
合同っぽい図形を見つける
合同っぽい三角形のペアを見つけて、三角形の合同条件を1つでも満たすか?確認する。
解き方
まず、角度を書き込む。三角形の内角の和は180°なので・・・!
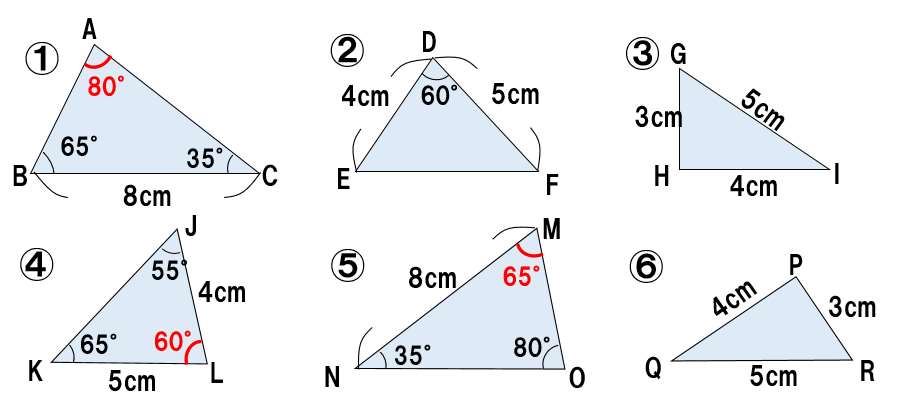
合同っぽい三角形のペアを見つけ出してね!
①と⑤に注目。
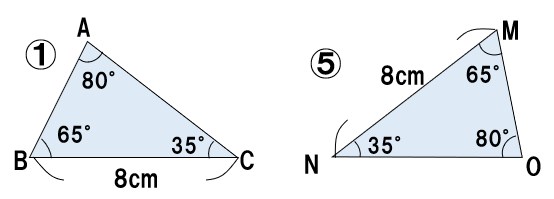
- BC=MN 辺が等しい
- ∠B=∠M 角が等しい
- ∠C=∠N 角が等しい
よって、1組の辺とその両端の角がそれぞれ等しいので、△ABC≡△OMN・・・(答え)
②と④に注目。
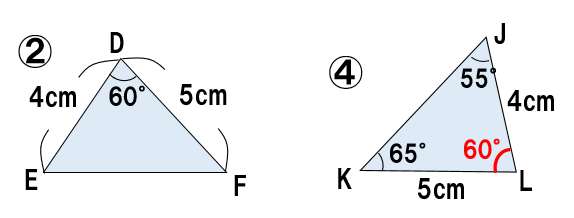
- DE=LJ 辺が等しい
- DF=LK 辺が等しい
- ∠D=∠L 角が等しい
よって、2組の辺とその間の角がそれぞれ等しいので、△DEF≡△LJK・・・(答え)
③と⑥に注目。
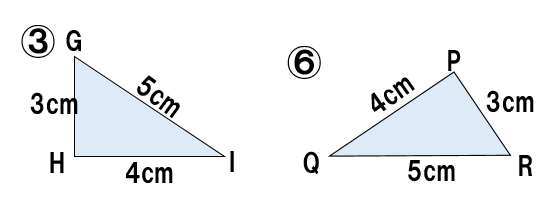
- GH=RP 辺が等しい
- HI=PQ 辺が等しい
- IG=QR 辺が等しい
よって、3組の辺がそれぞれ等しいので、△GHI≡△RPQ・・・(答え)
はい、次の問題!
つぎは、みんな苦手の「証明問題」まずは証明の基礎を理解しよう