ポイント
水槽の水の量を具体的に書いてみよう！
この手の問題はイメージする＆具体的数字でとりあえず書いてみることが、とても大切！
文字がたくさん出てくると、混乱しちゃうね？だから、具体的な数字を書いてみればいいんだ！
そうするとイメージできる！こんな感じでね
↓↓
ｘ分後の水槽に残っている水の量がｙだから、ｘとｙの関係を書いてみよう！
| ｘ | ｙ |
| 0分後 | 100ｍ3 |
| 1分後 | 98ｍ3 |
| 2分後 | 96ｍ3 |
| 3分後 | 94ｍ3 |
| 4分後 | 92ｍ3 |
| ・・・ | ・・・ |
こうやって、具体的にイメージできるようにすることが大切なんだ！！！
具体的なことが何で大事なのか？それはｙをｘで表すときに活躍する！最後まで見たらわかる！
解き方
ｘの変域
ｘの変域とは「ｘが変化する範囲」だったね？
●≦ｘ≦▲ などで表されるよ！
じゃあ、問題をよく見てみよう！
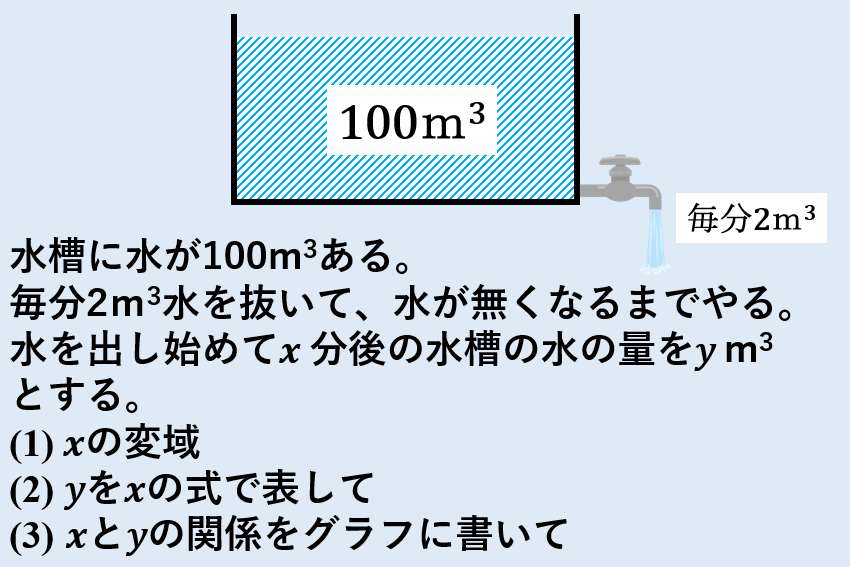
- 水が100ｍ3 入っている
- 毎分2ｍ3 水を抜く
- 水が無くなるまで抜く
- 水を出し始めてｘ分後の水槽の水の量がｙ
ということは、
ｘの変域は、水を出し始めてから、無くなるまでの時間だね？
- 出し始め時間：0分
- 無くなる時間：50分（100m3 ÷ 2ｍ3 =50分）
つまり、xの変域は
0≦ｘ≦50・・・（答え）
ｙをｘの式で表せ
ｙ＝●ｘ+▲ と表すのがゴールだよね？
思い出してほしい、１番最初にイメージしたことを！これ
↓↓↓
- 0分後→100ｍ3
- 1分後→98ｍ3
- 2分後→96ｍ3
- 3分後→94ｍ3
じゃあ、ｙをｘで表す準備をするよ・・？
0分のとき、水槽には100ｍ3の水がありました。
だからまずは、ｙ＝100
１分ごとに2 (ｍ3)減ります。この考え方を元にyを表してみると・・・
- 0分後：100ｍ3 → ｙ＝100
- 1分後：98ｍ3 → ｙ＝100-2×1
- 2分後：96ｍ3 → ｙ＝100-2×2
- 3分後：94ｍ3 → ｙ＝100-2×3
でね、もう答えが出てるんだ！
1分2分3分・・・ていうのは、「ｘ」のことだよね？？
だから、ｘに替えてしまえばOK！！！！！
答えは、ｙ= 100 – 2x
ちょっとカッコよく変形すると、ｙ= – 2x +100・・・（答え）
ｘとｙの関係をグラフに書け
下のようなグラフ用紙が与えられているとしましょう！
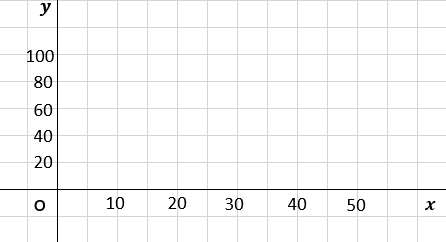
さ、グラフを書いてみよう！！
ｙ= – 2x +100
まずｘ＝0のときの切片は、ｙ＝100だね。プロットしよう
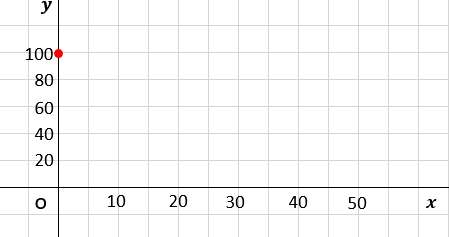
ｘ＝10のときは、ｙ＝-2×10+100＝80だ！！
だから（ｘ,ｙ）＝（10 ,80）をプロットする。
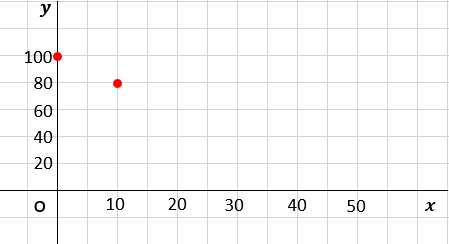
ｙ= – 2x +100のグラフは、右肩下がりの直線なので、あとはこの２点を結ぶだけで完成！
ｘの変域、0≦ｘ≦50に注意してグラフを作成するとこうなる
↓↓
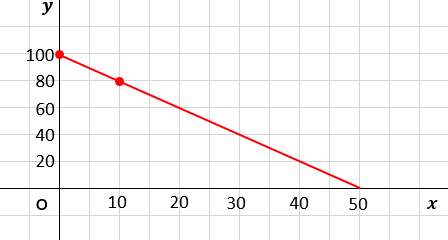・・・（答え）
グラフを見ると、50分後に水槽の水が0になっていることが、きちんと確認できるよね！
（逆に、50分後に0になっていないとグラフが間違っているよ）
次の問題！次から章が変わって、角度（同位角・錯角・平行線）の分野だ！
まずは基礎を理解しよう
