もくじ
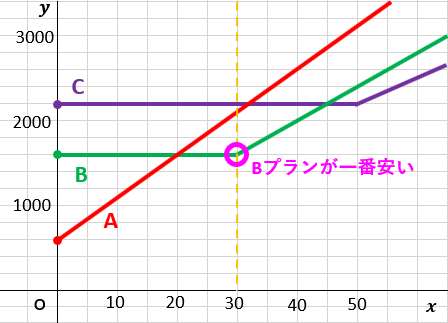
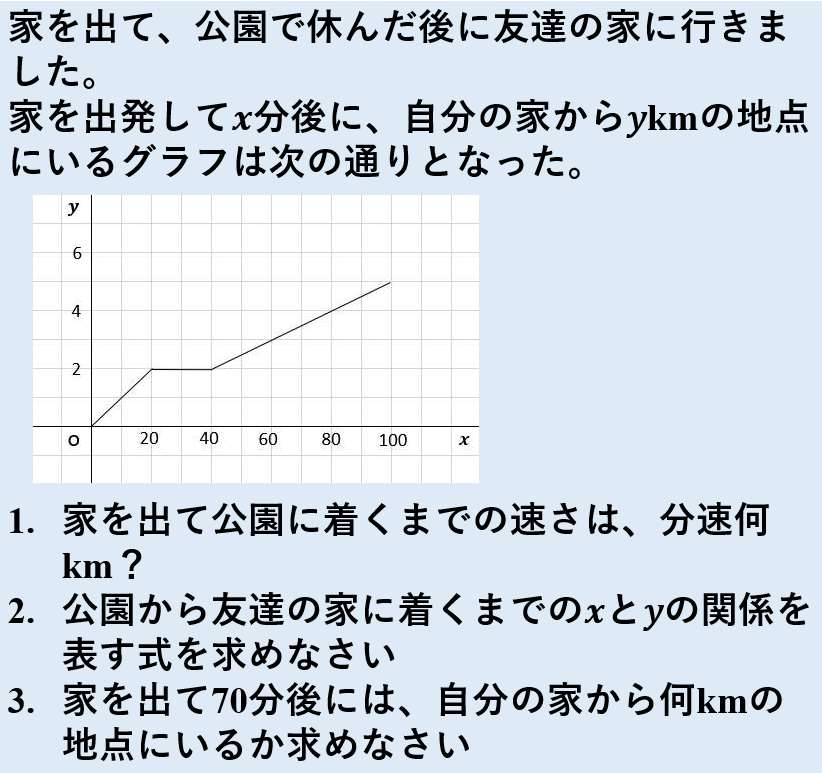
問題
ポイント
- ｘ軸ｙ軸の１目盛りが「１」とは限らない
- グラフの傾き変わるポイント＝速さが変わるポイント
- 「速さ」を求めよ→グラフの「傾き」を求める
- ｘとｙの関係式→２点の座標から求める
ｘ軸ｙ軸の１目盛りが「１」とは限らない
前回も言ったけど、お金、速さ、水の量などの問題は、グラフの１目盛りが「１」とは限らない！
１目盛り分がいくらの値なのか、きちんと確認しよう！
グラフの傾き変わるポイント＝速さが変わるポイント
グラフの傾きが変化する＝速さが変わるポイント！
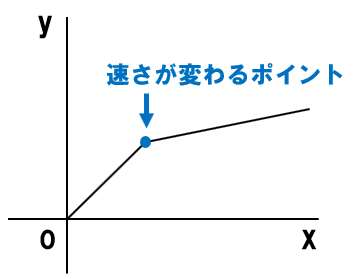
グラフの傾きが「0」＝移動していない、つまり休憩だ！
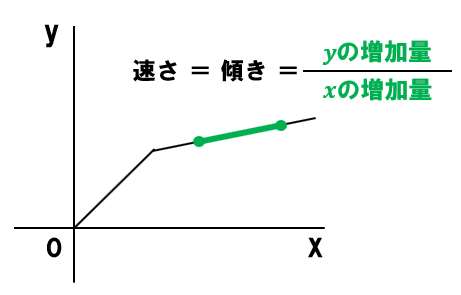
「速さ」を求めよ→グラフの「傾き」を求める
「速さ」は「直線の傾き」
グラフ上の２点から、直線の傾きを求めよう！
ｘとｙの関係式→２点の座標から求める
求める直線の中で、整数である２点の座標を選ぼう！
この２点の座標がわかったのであれば、「ｙ＝ほにゃららｘ」の形を作ることができるね？
解き方
個別問題を解く前に・・・！
問題を解く前の手順
- ｘ軸ｙ軸の目盛りを確認しよう
- 到達地点をグラフに書いてしまおう
＜目盛り確認＞
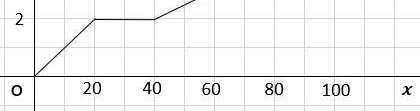
- ｘ軸の１目盛りは、10分
- ｙ軸の１目盛りは、1ｋｍ
＜到達地点をグラフに書く＞
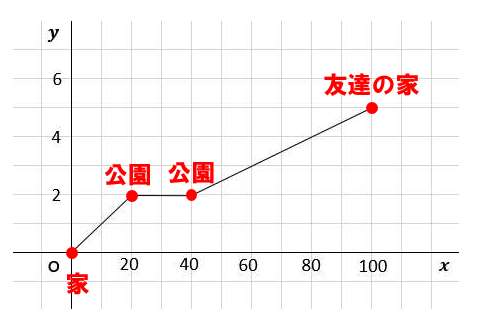
速さを求める問題だ！！これを思い出して！
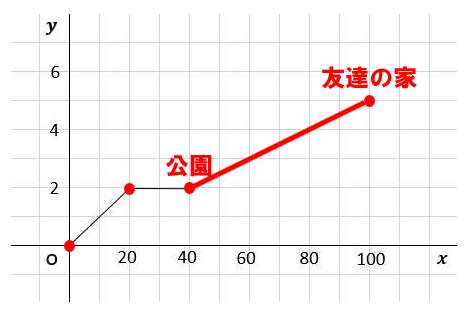
家から公園までを表すのは下の図の緑部分だね。この傾きを求める。
２点（0、0）（20、2）を通ることに着目して
速さを求める式は
計算すると、分速0.1km・・・（答え）
ｘとｙの関係式→２点の座標から求めるんだったね！
公園を出るとき、友達の家に着くときの２点の座標は
（ｘ、ｙ）＝（40、2）（100、5）
この２点を通る直線は、
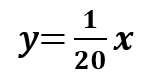・・・（答え）
「２点の座標から直線の式を求める方法」がわからなければ、ココをもう一度見て復習！
家を出て70分後の位置は、
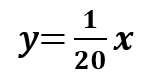の直線上の点だよね？？
だから、ｘ＝70を代入して
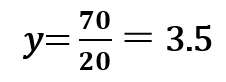
よって、家を出てから70分後には、自分の家から3.5km地点にいる・・・（答え）
さあ次！これも頻出！ろうそく問題だ！！
理解できた？
