【動画解説】
もくじ
ポイント
- グラフ「1目盛り」の数値を確認しよう
- 切片は基本料金
- 基本料金だけでOKなのは、通話時間が何分まで?
- 基本料金以降は、yはxに比例する
グラフ「1目盛り」の数値を確認しよう

今までみんなが作図してきたグラフは
- 1目盛り=1
だったよね??
ところが、
お金の金額や、時間、距離に関するグラフは、「1目盛り=1」ではないケースが多いよ!
グラフの目盛りは、問題や解答用紙に書いてあるので、1目盛りがいくらの数値なのか、正確に見極める必要があるよ!
切片は基本料金
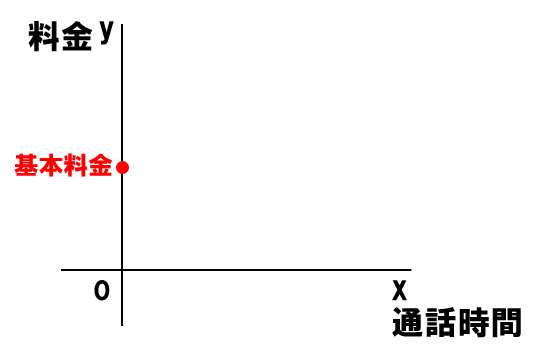
切片のy座標は、基本料金の数値になる!!
なぜなら、
x=0(通話時間0分)のとき、基本料金だけは掛かるからだね!
もし、基本料金が無料なら、切片のy座標は0になるね。
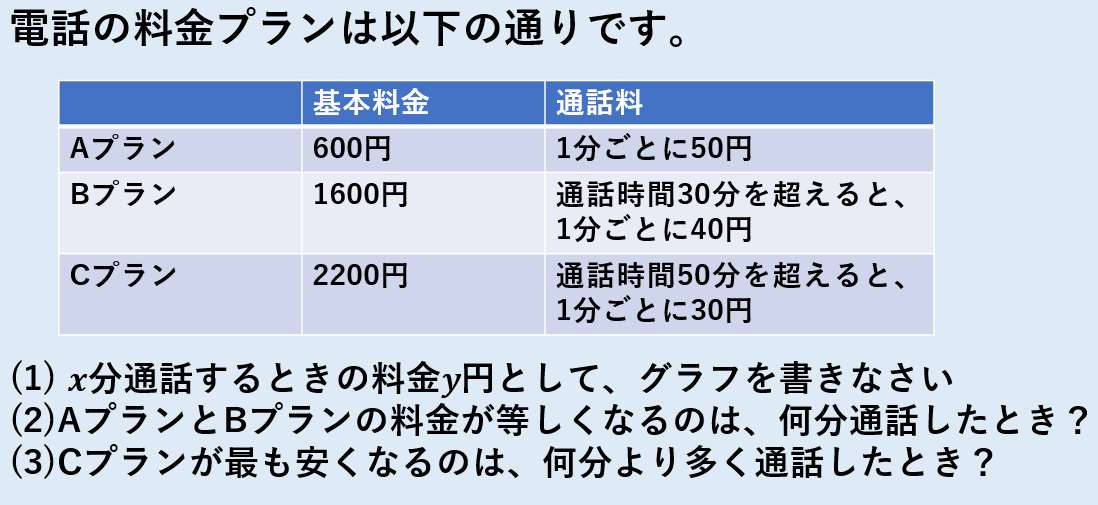
基本料金だけでOKなのは、通話時間が何分まで?
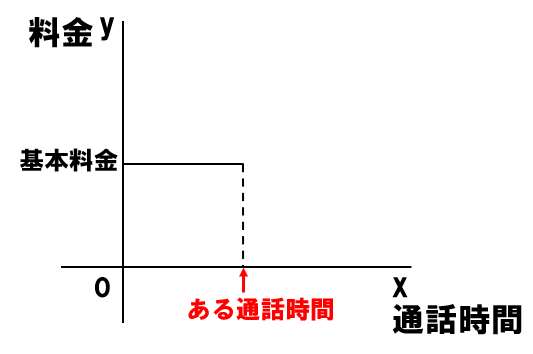
「ある通話時間」までは、基本料金だけで電話をかけることができる。
では、「ある通話時間」とは?もう一度、それぞれのプランに必ず記載があるので確認しよう!
●●分を超えると、1分ごとに料金がかかる。という文章の「●●分」が「ある通話時間」だよ☆
基本料金以降は、yはxに比例する
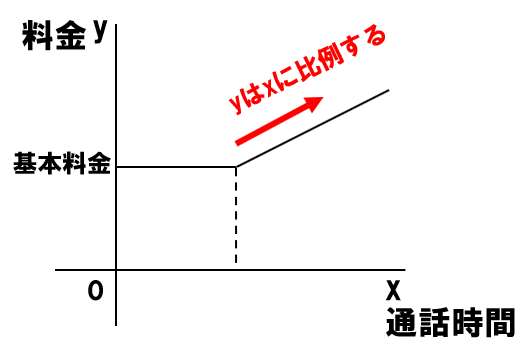
解き方
![]()
- ステップ1:グラフ「1目盛り」の数値を確認しよう
- ステップ2:切片の座標をプロット
- ステップ3:基本料金だけでOKな範囲をグラフに書こう
- ステップ4:グラフを完成させよう
グラフ「1目盛り」の数値を確認しよう
こういった料金問題では、グラフの目盛りが通常と異なるので注意してね!
ここでは、与えられた方眼紙が次の通りだとしよう。
このグラフから、次の通り読み取れる。
- x軸の1目盛りぶんは:5分
- y軸の1目盛りぶんは:200円
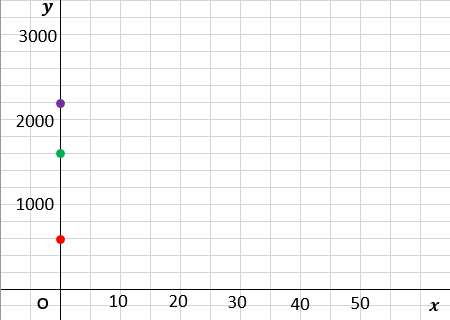
切片の座標をプロット
分かりやすくするために、各プランを色分けしてみたよ。
切片のy座標は、基本料金の数値になる。と言ったよね?
なので、まずは切片をプロットしてみよう!
(Aプラン:赤、Bプラン:緑、Cプラン:紫)
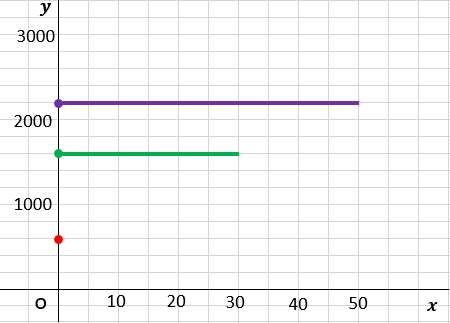
基本料金だけでOKな範囲をグラフに書こう
基本料金だけで電話できる「ある通話時間」は
- Aプラン → 0分まで
- Bプラン → 30分まで
- Cプラン → 50分まで
なので、
- Aプラン → 0分から0分まで、600円
- Bプラン → 0分から30分まで、1600円
- Cプラン → 0分から50分まで、2200円
だからこれをグラフに書く!
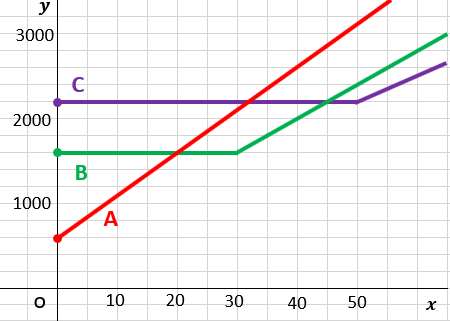
グラフを完成させよう

基本料金以降は、
- Aプラン:1分ごと50円
- Bプラン:1分ごと40円
- Cプラン:1分ごと30円
x軸の目盛りの最小は5分なので、1分はプロットしにくいね??
だからとりあえず、10分ごとの通話料の変化でプロットすることにしよう。
すると
- Aプラン:10分ごと500円 →(xに10進んで、yに500進む)
- Bプラン:10分ごと400円 →(xに10進んで、yに400進む)
- Cプラン:10分ごと300円 →(xに10進んで、yに300進む)
これをプロットしよう!
 ・・・(答え)
・・・(答え)
![]()
グラフより、20分・・・(答え)
![]()
Cプランが最も安くなる通話時間 → xが同じのときCプランのグラフが一番下に来る通話時間は??
例えば、15分では?
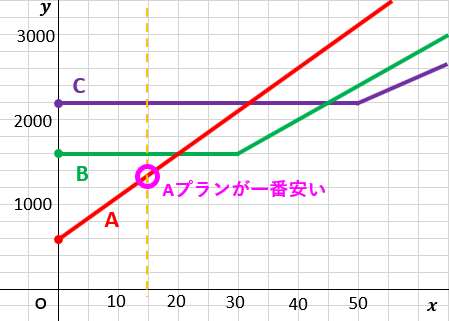
例えば、30分では?
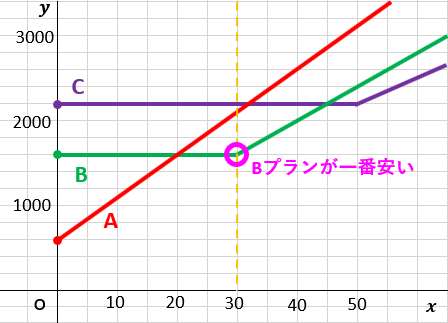
45分でようやくCプランが最も安くなる。
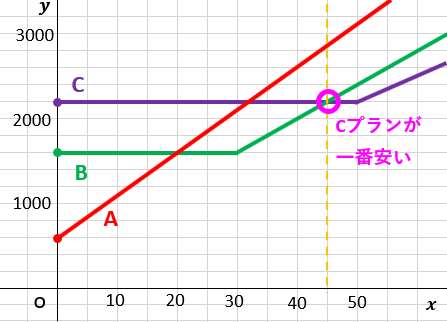
よって、Cプランが最も安くなるのは45分より多く通話したとき・・・(答え)
さあ、次!似たような問題で実力を付けて行こう!歩く距離と時速のグラフ問題だ。