中２数学：文字式の利用（奇数から偶数をひくと奇数）

問題

奇数から偶数をひいたら「奇数」になる。
その理由は？

基礎的な問題だけど、なにより基礎が重要！絶対理解すべき内容なので、確実に解けるようにしよう！！！

解法手順

1. 偶数・奇数を文字を用いて表す
2. 問題の言う通りする
3. ゴールの形に

解くための基礎知識

• 偶数は、「２」でわりきれる数
• 奇数は、「２」でわりきれない数

これはOKだよね？？

だから、

• 偶数は、２×●
• 奇数は、２×▲+1

と表すことができるよね？？？

（●や▲は、適当な正の数だよ）

これを文字式を用いて表すとこうなる。

↓↓

mとnを整数とすると

• 偶数　→　2m
• 奇数　→　2n+1

でも注意！！

これはNGです

↓↓

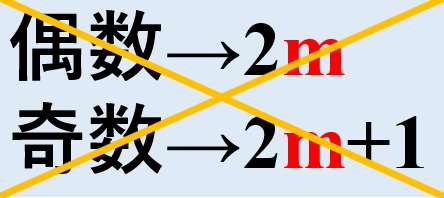
奇数と偶数を、同じ「ｍ」を用いてはダメなんだ！

なぜなら、

• 2m
• 2m+1

これだったら、連続した２つの偶数と奇数になってしまうからね。

（16と17、48と49、60と61・・・とか）

「ランダムな」偶数と奇数にはならないからね！！

奇数と偶数は、異なる文字であらわすこと！

解法

偶数・奇数を文字を用いて表す

mとnを整数とすると

• 偶数　→　2m
• 奇数　→　2n+1

問題の言う通りする

問題の通り、

言われた通り、奇数から偶数をひいてみよう。

(2n+1)-2m

=2n-2m+1

ゴールの形に

ゴールの形は、「奇数」だよね？？

始めに言ったこと、思い出して！

• 偶数は、２×●
• 奇数は、２×▲+1

だから、目指すべきはこの形

↓↓

この形に変形するんだ！！！！

で、ついさっきの式を変形してみよう！

2n-2m+1

＝2(n-m)+1

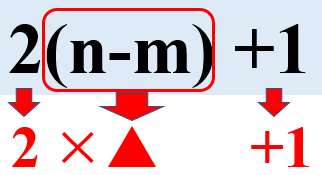
これで完成！

だって、

(n-m)は整数だから、2(n-m)は偶数。

よって、2(n-m)+1は奇数となる。

補足

ちなみに、奇数の置き方は、以下の通りでもOKだよ！

• 偶数　→　2m
• 奇数　→　2n-1

としてもOK！

奇数から偶数をひくと

(2n-1)-2m

=2(n-m)-1

n-mは整数だから、2(n-m)は偶数。

よって、2(n-m)-1は奇数となる。