もくじ
多角形の内角の和
みんなが今まで学んできたのは、「三角形」の内角外角だったね??
そして、三角形の内角の和は360°だったね??
じゃあ、四角形の内角の和は??五角形の内角の和は??・・・さぁ学習していこう!!
四角形の内角の和
答えは、360°なんだ。
なんでかって??
それは、2つの三角形を組み合わせて、内角の様子を観察するとわかるよ!!
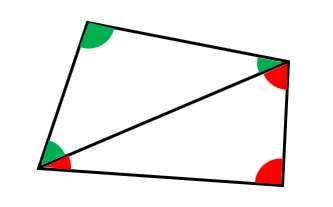
- 緑の内角の和:180°
- 赤の内角の和:180°
- 緑+赤の内角の和:360°(180°+180°)
緑+赤の内角の和は360°だよね?これって、結局、四角形の内角の和のことを言っているわけ!
ほんじゃ次!
五角形の内角の和
答えは、540°なんだ。
同じように五角形の内角の和を考えてみる!
四角形と全く同じやり方で、五角形を三角形に分けてみよう!!こんな感じで↓↓
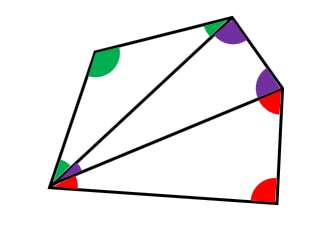
すると、
- 緑の内角の和:180°
- 紫の内角の和:180°
- 赤の内角の和:180°
- 緑+紫+赤の内角の和:540°(180°+180°+180°)
ほにゃらら角形の内角の和は??
じゃあ、ほにゃらら角形の内角の和はどうなるか?考えてみよう!
ほにゃらら角形は表現しにくいので、ここでは「★角形」と表現していくよ!
始めに答えを言ってしまおう!
「★角形」の内角の和は、180°×(★- 2)だよ!
これまで考えてきたことを表にしてみよう!
【内角の和】
| 3角形 | 4角形 | 5角形 | ★角形 |
| 180° | 360° | 540° | 180°×(★- 2) |
5角形だったら、180°×(5-2)をすればいいんだ。ちゃんと540度になるよね?
問題
理解度を確かめる基礎的な問題を解いてみよう!
①12角形の内角の和は?
「★角形」の内角の和は、180°×(★- 2) だったね?
だから、12角形の内角の和は
180°×(12 – 2)=1800°・・・(答え)
②正12角形の1つの内角の大きさは?
正12角形というのは、内角が全て同じ大きさだね?
(正3角形は、内角がすべて同じ(60°)というようにね!)
だから、正12角形の1つの内角の大きさは
1800°÷12=150°・・・(答え)
③内角の和が、1260°である多角形は何角形?
「★角形」の内角の和は、180°×(★- 2)だったね??
★角形では、ダサいので、求める多角形を「n角形」としてみよう。
内角の和が1260°なので、次の式が成り立つ
180°×(n- 2)=1260°
よってn=9、つまり求める多角形は、9角形・・・(答え)
④へんてこ図形の内角の和は?
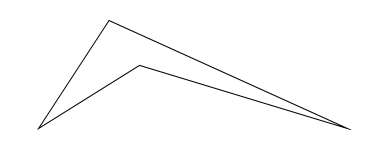
わかる??
これ、4角形だよね?辺が4つあるから。
4角形なので、内角の和は、180°×(4 – 2)=360°・・・(答え)
どんなヘンテコ図形でも、(曲線とかが存在しない限り)内角の和の式は、当てはめてOKなんだ!
多角形の外角の和
多角形の外角の和は360°になる(どんな多角形でも360°)
例えば四角形なら
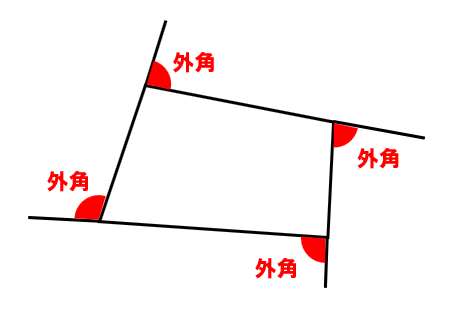
ちなみに、1つの頂点に対して、外角は2パターンあるよ!
例えば左上の頂点では
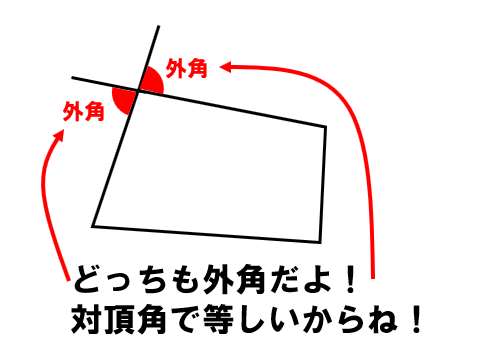
どちらを選んでも、同じ頂点の外角は等しいよ!(対頂角だから!!)
外角の和をド忘れしてしまったら・・?
多角形の外角の和は360° と覚えたけど、もしも、忘れてしまったら・・?
多角形ってことは、3角形も含まれる。ってことで、正三角形を考えてみればいいんだ!
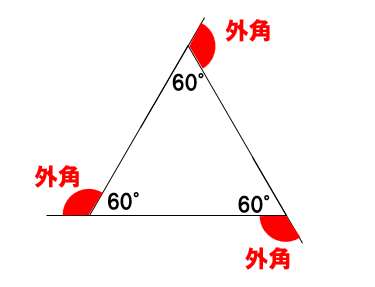
正三角形の1つの内角は60°、外角は120°なので、
外角の和は120°×3=360°
「あっ、そうそうそうそう、外角の和は360°だったね~」 と思い出そう!!
- 多角形の外角の和を忘れたら、正三角形で検証せよ!!
問題
①∠xを求めよ
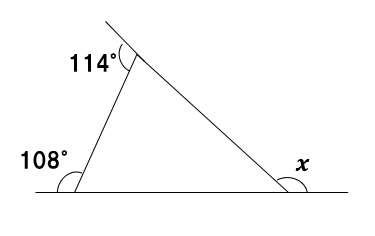
図に示された角度は、全て三角形の外角だね?
三角形の外角の和は360°なので
∠x=360° -(114°+108°)=138°・・・(答え)
②∠yを求めよ
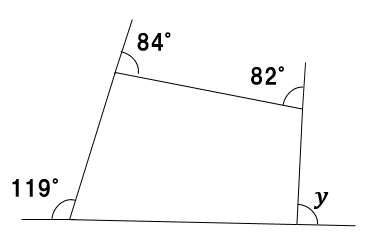
同じく、図に示された角度は、全て四角形の外角だね?
四角形の外角の和は360°なので
∠y=360° -(119°+84°+82°)=75°・・・(答え)
③正12角形の1つの内角の大きさは?
解法1:外角を用いた解法
正12角形の外角の大きさは全て等しく、外角の和は360°。
だから、1つの外角の大きさは360°÷12=30°
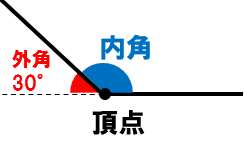
1つの頂点において、内角+外角=180°となるので
1つの内角の大きさは 180°-30°=150°・・・(答え)
解法2:内角を直接求める解法
最初にやったことを思い出して!
「★角形」の内角の和は、180°×(★- 2)だったね
じゃあ、正12角形の内角の和は、180°×(12 – 2)=1800°だね??
正12角形は、すべての内角が等しいので、1つの内角は
1800°÷12=150°・・・(答え)
さあ、次の問題!合同だ!三角形の合同条件まとめ