もくじ
三角形の内角
三角形の3つの内角の和 → 必ず180°になる
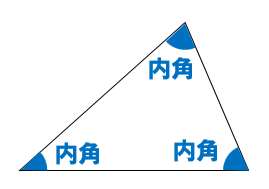
問題
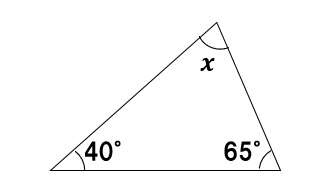
xの角度は??簡単だね?3つの内角を全て足し算すると180°だから、
40°+65°+∠x=180°
∠x=75°・・・(答え)
三角形の外角
赤色の角度のことを、ぜんぶ「外角」と呼ぶよ!
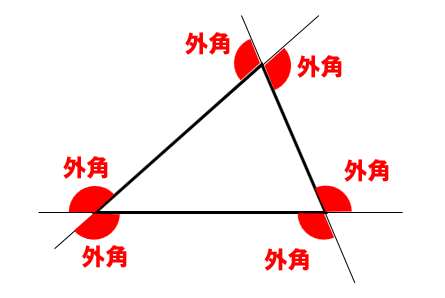
三角形の1辺を延長して外角を理解しよう!
三角形の1つの外角は、その隣にない2つの内角の和と等しい
はい。これ意味わかる・・・?クソわかりづらいよね?ウンウン。。
下の図で解説しよう!
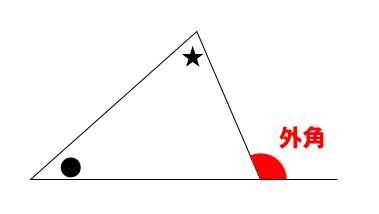
- 三角形の1つの外角 → 赤色の外角のこと
- その隣にない2つの内角の和 → ●+★
だから、外角の大きさ=●+★ ってこと!
ホント・・??じゃあ、この三角形の外角を求めてみよう!
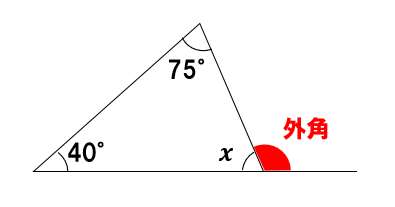
外角の求め方①
外角は直線上にある。三角形の内角の和は180°なので、∠xを求めると
40°+75°+∠x=180° → ∠x=65°
外角と∠xの和は、180°(直線だから)なので、
∠外角=180°- 65°=115°・・・(答え)
外角の求め方②
外角の大きさ=●+★ を使ってみよう。
∠外角=40°+75°=115°・・・(答え)
ほら同じになるでしょ?!
だから
三角形の1つの外角は、その隣にない2つの内角の和と等しい
外角は対頂角になっている
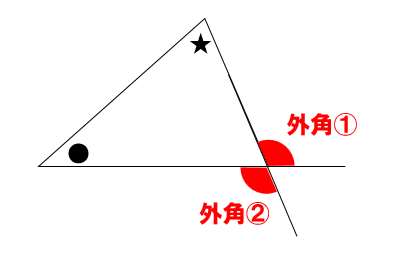
このように、外角①と外角②は向かい合っている。つまり対頂角なんだ!
忘れている人は思い出して
↓
だから、
∠外角①=∠外角② なんだ。
つまり、以下2つはどっちも成り立つわけ!
- ∠外角①=●+★
- ∠外角②=●+★
三角形の内角と外角のまとめ図
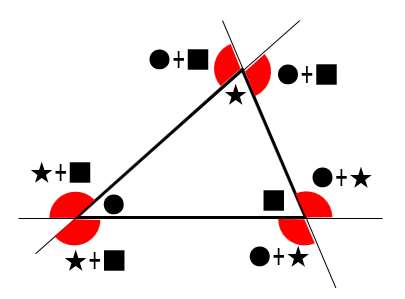
これを理解していれば、三角形の内角・外角は完璧!
問題
問題①
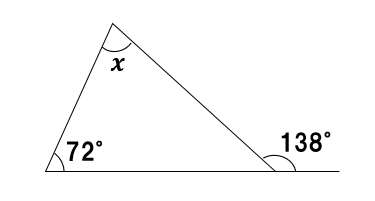
外角が138°だ。だから
∠x+72°=138°
∠x=66°・・・(答え)
問題②
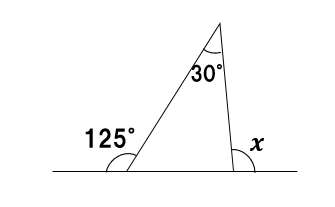
これは一筋縄ではいかないね?こういう時は、計算で求められる角度があるはずだ。
求めることができる角度はコレ↓↓
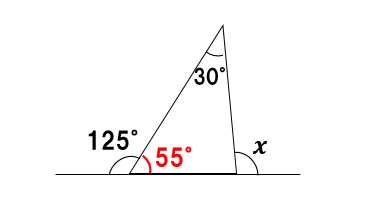
三角形の外角と内角の関係から、
55°+30=∠x
よって∠x=85°・・・(答え)
問題③
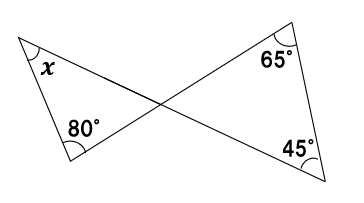
こいつも一筋縄ではいかねーな!
右側の三角形で、三角形の外角と内角の関係を利用しよう。
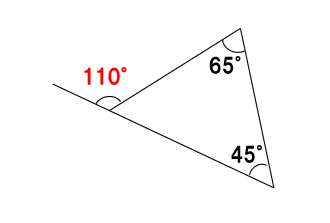
65°+45°=110°
次に、左の三角形に着目すると・・
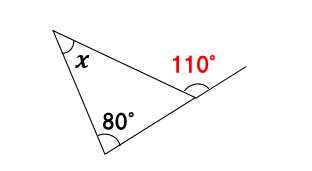
同じように三角形の外角と内角の関係を利用して
80°+∠x=110°
よって∠x=30°・・・(答え)
問題③の別解
外角の性質を利用して求めるのが理想だけど、始めはパッと思いつかないかもしれない。
こんな感じで別の解き方もあるよ!
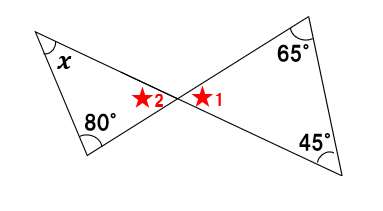
- まず右の三角形の内角の和180°を利用して、★1を求める。
- ★1と★2は対頂角なので等しい
- 左の三角形の内角の和180°を利用して、∠xを求める
どちらで解いてもOK!もちろん答えは同じ。
慣れてきたら、なるべく外角の性質を利用して解く方がスマートだね。
三角形の種類(鋭角、直角、鈍角)
三角形には3つの種類があるよ。
- 鋭角(えいかく)三角形
- 直角三角形
- 鈍角(どんかく)三角形
で、その前に、
- 鋭角:90°よりも小さい角度のこと(0°よりは大きい)
- 直角:90°のこと
- 鈍角:90°よりも大きい角度のこと(180°よりは小さい)
覚え方。
鋭角というのは、鋭(するどい)と訓読みするよ。全ての角が、するどくとがっている → 鋭角と覚える
ドンくさいって言葉しってるかな??
遅い、のろい、トロいとかいう意味だね。(あまりいい意味では使わないよ。)
だから、なんとなく、だらしな~い角度 → だら~っとした大きな角度 → 鈍角と覚える
それぞれの三角形の分類方法
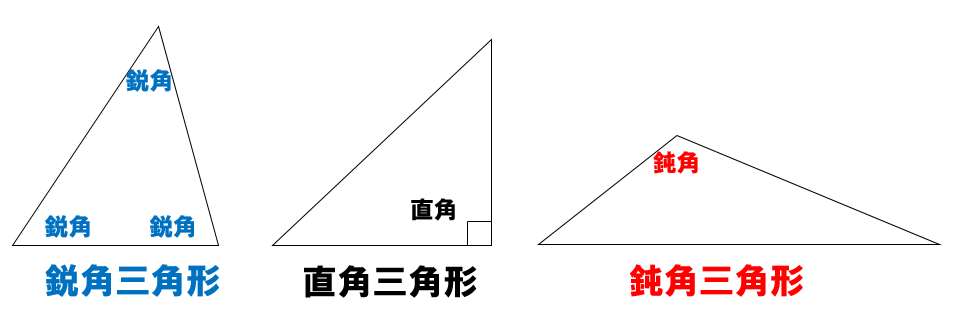
- 鋭角三角形:3つの内角すべてが鋭角
- 直角三角形:1つの内角が直角
- 鈍角三角形:1つの内角が鈍角
何三角形??見極め方ポイント
- ステップ1:内角に直角がある → Yes:直角三角形 No:ステップ2へ
- ステップ2:内角の1つが鈍角だ → Yes:鈍角三角形、No:鋭角三角形
よし、次!三角形の後は、四角形、五角形・・・多角形について!